Headed to Beijing, back for dinner!
The gravity train is a hypothetical idea proposed by Robert Hooke (he of Hooke's law fame) to Isaac Newton in the 1600's. It consists of a simple idea that's hard to implement in practice. Dig a tunnel that runs straight through Earth between two points on the surface. If you can figure out how to remove friction and lower air resistance, you now have a mechanism for extremely efficient and rapid travel between widely separated points. Simply drop something into the tunnel at one end. Gravity will initially pull it downwards through the tunnel, eventually reaching high speeds. Once the object is halfway through the tunnel, gravity will now slow it back down, so you can retrieve the object easily on the other side.
While there are obvious engineering impracticalities, it winds up being pretty amazing how fast a gravity train can get things from point to point without needing fuel. So, let's say we wanted to go from Beijing to Paris using such a gravity train. How long does the trip take assuming a frictionless and drag-free train to the nearest minute ?
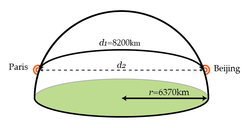
Earth can be modeled as a sphere of uniform density, with total mass 6 × 1 0 2 4 kg and radius 6 3 7 0 km . The shortest distance from Beijing to Paris on the surface of Earth is approximately 8 2 0 0 km .
Details and Assumptions:
- Newton's constant is 6 . 6 7 × 1 0 − 1 1 N m 2 / kg 2 .
- The mass of the Earth is 6 × 1 0 2 4 kg .
The answer is 42.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
5 solutions
Every time I was posting, I forgot to divide by 2. :(
Let us say the perpendicular distance of the line connecting the points from center of earth is h . At a distance r from center , Force experienced = R 3 G M m r = R g m r .
Now , say we are going from beijing to paris and denote x as the distance from the center of line L connecting them towards beijing , hence towards paris x would be negative.
Say the angle made by line connecting center to the train with h is θ .Note that we would consider force along L only .Also, r = c o s θ h
F x = R g m c o s θ h s i n θ = R g m h t a n θ = R g m x
This clearly represents SHM , whose time period ( T ) = 2 π g R .
Hence, time taken = 2 T = π g R = 4 2 (min.)
Don't you think the heading of question is great ?
Suppose when the distances from the train to the center of the Earth and the middle point of d 2 are d and x respectively.
We know that the part with R > d does no force on the train, only the part with R ≤ d does gravitational force on the train:
F = d 2 r 3 G m M d 3 = r 3 G m M d .
Therefore, m x ′ ′ = − F cos α = − r 3 G m M d d x = − r 3 G m M x .
x ′ ′ + x r 3 G M = 0 .
Therefore, time to travel does not depend on the position of the destination and will be:
t = 2 T = π G M r 3 = 4 0 ( m i n s )
you missed the square root.
Log in to reply
Yes, I forgot to put it. And a typo, in the last line, it's 42, not 40.
Let the center of the Earth be O , and the midpoint of the tunnel be M . At time t , let the position of the train be given by P ( t ) , and let the angle ∠ O M P ( t ) be given by the function θ ( t ) . If the (directed) distance from P ( t ) to M is given by the function x ( t ) , then note that x ( t ) = ± r ( t ) cos ( θ ( t ) ) , where r ( t ) is distance from the center of Earth to the train. Let M ( r ( t ) ) be the mass of the portion of Earth below the train at time t . Then, note that M ( r ( t ) ) = ρ 3 4 π r ( t ) 3 where ρ is the density of the Earth. By Newton's law of of gravitation, the gravitational force acting on the train at time t will be: F ( t ) = − G 3 4 π ρ m r ( t ) (where m is the mass of the train) We now decompose this force into two components: one acting along the tunnel, the other acting along the vertical. The latter is cancelled by the reaction force of the rail. We are concerned only about the component of F ( t ) acting along the rail, which is F ( t ) cos ( θ ( t ) ) . The equation of motion of the train will then be: m x ( t ) ′ ′ = F ( t ) cos ( θ ( t ) = − G 3 4 π ρ m x ( t ) (since x ( t ) = ± r cos ( θ ( t ) ) ) Note that this is very similar to the equation of a linear oscillation with half period k = 3 4 π ρ G π . Note that here the half period corresponds to the time of a one way trip. Plugging the given values (note: ρ = 3 4 π R 3 M where R is the radius of the Earth), we obtain the time ≈ 4 2 minutes .
Two interesting notes:
i)
Note that the time of travel is independent of the distance travelled. This implies in a gravitational train, the time taken to reach Antarctica will be the same as the time taken to go to my neighbor's house. :)
ii)
Note that the time travelled will be the same for all planets with the same density, no matter how large or small that planet is. :)
Typo: F ( t ) = − G 3 4 π / R ( t ) 2
Let x be the distance of the train from the midpoint of the tunnel (the point nearest the centre of the Earth), and let y be the distance of the train from the centre of the Earth. The gravitational force on the train at that point is due to the sphere of the earth that is closest to the centre of the earth than the train, namely a sphere of radius y , and hence of mass r 3 y 3 M , where r is the radius of the earth. Thus the gravitational force acting on the train is F = r 3 y 2 G y 3 M m = r 3 G y M m , where m is the mass of the train. The component of the force along the tunnel is F × y x = r 3 G M m x . Thus the equation of motion of the train is m x ¨ = − r 3 G M m x In other words, the train performs SHM with ω 2 = r 3 G M . The journey time is half a period, namely π G M r 3 The journey time is the same for any destination, and (to the nearest minute) this is 4 2 minutes.
Let us assume:
From this, our radial force is
F r = G r 2 m M ( r )
where M ( r ) = 3 4 π ρ E r 3 at a certain distance r away from the center of the Earth. This is the mass of the sphere with radius r .
Therefore, the horizontal component of the gravitational force is
F x = F r sin ( α ) = 3 4 π ρ E G m r sin ( α ) = 3 4 π ρ G m x
since the horizontal force is opposite to our positive x-direction
F x = − 3 4 π ρ G m x
so we have
m x ¨ + 3 4 π ρ G m x = 0
On Earth's surface,
g = 3 4 π ρ G R
so we can simplify our equation to
x ¨ + R g x = 0
This describes the oscillation motion for the frequence Ω = R g
so the time it takes to get to Paris, or half the oscillation period is, T = π g R ≈ 2 5 4 0 s ≈ 4 2 m i n u t e s