Health Insurance (Part 2)

Probability Level 2

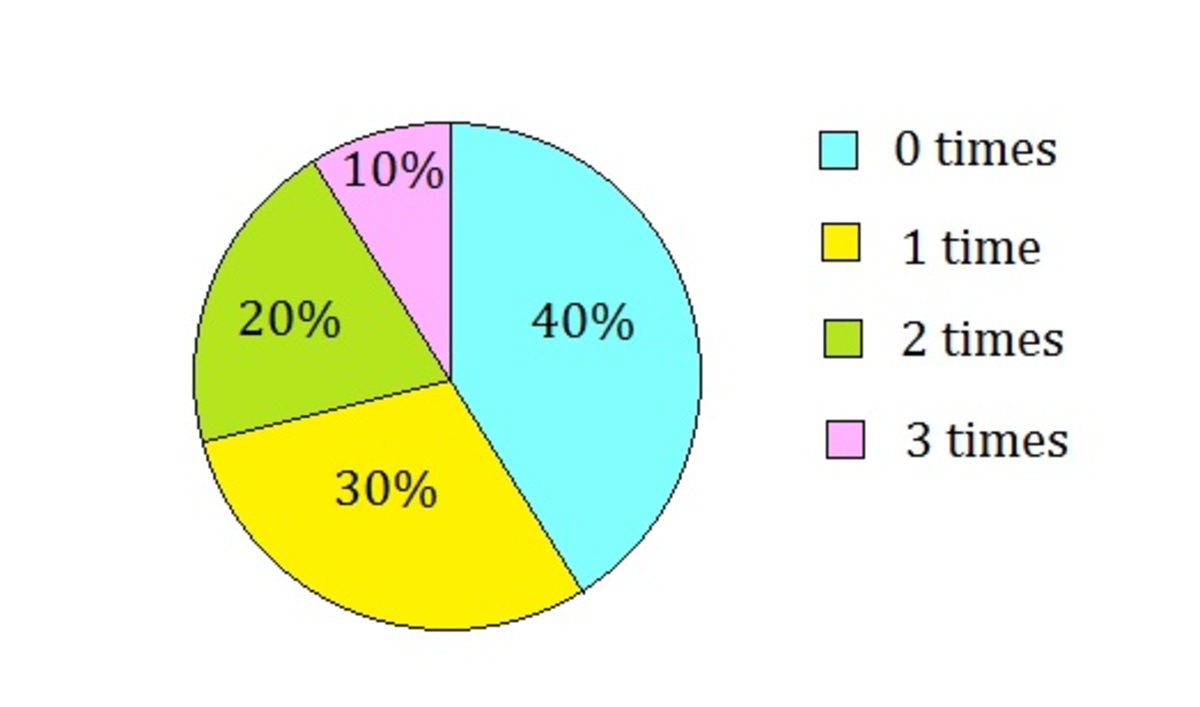
An insurance company has reviewed the number of times their clients have claimed for their hospital coverage in the past year, and all the data are presented in the pie chart above.

What is the variance of number of claims among these clients?


The answer is 1.

View wiki
Worranat Pakornrat by Worranat Pakornrat , 36, Thailand

This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try refreshing the page, (b) enabling javascript if it is disabled on your browser and, finally, (c) loading the non-javascript version of this page . We're sorry about the hassle.

1 solution

In order to find the variance, we need to determine the mean of claims first.

Let N N be the total number of clients of this company.

Hence, the total numbers of times they have used the insurance

= 0 × ( 40 100 ) N 0\times(\frac{40}{100})N + 1 × ( 30 100 ) N 1\times(\frac{30}{100})N + 2 × ( 20 100 ) N 2\times(\frac{20}{100})N + 3 × ( 10 100 ) N 3\times(\frac{10}{100})N

= N N

Therefore, the average times of insurance claims = N N \dfrac{N}{N} = 1 .

In other words, in the past year, the clients have averagely used their insurance only once. The mean is 1.

Now the variance = ∑ ( ( x − μ ) 2 N ) \sum (\dfrac{(x - \mu)^2}{N})

= ∑ ( ( x − 1 ) 2 N ) \sum (\dfrac{(x -1)^2}{N})

= ( 0.4 N ) ( 0 − 1 ) 2 + ( 0.3 N ) ( 1 − 1 ) 2 + ( 0.2 N ) ( 2 − 1 ) 2 + ( 0.1 N ) ( 3 − 1 ) 2 N ) \dfrac{(0.4N)(0 - 1)^2 + (0.3N)(1 -1)^2 + (0.2N)(2 - 1)^2 + (0.1N)(3 - 1)^2 }{N})

= 0.4 N + 0 + 0.2 N + 0.4 N N \dfrac{0.4N + 0 + 0.2N + 0.4N}{N}

= 1 .

Therefore, the variance of claims is also equal to 1 \boxed{1} .

2 Helpful 0 Interesting 0 Brilliant 0 Confused

Moderator note:

Simple standard approach.

Thank you for the review. ;)

Worranat Pakornrat - 5 years, 3 months ago

0 pending reports

×

Problem Loading...

Note Loading...

Set Loading...