Heat - 3
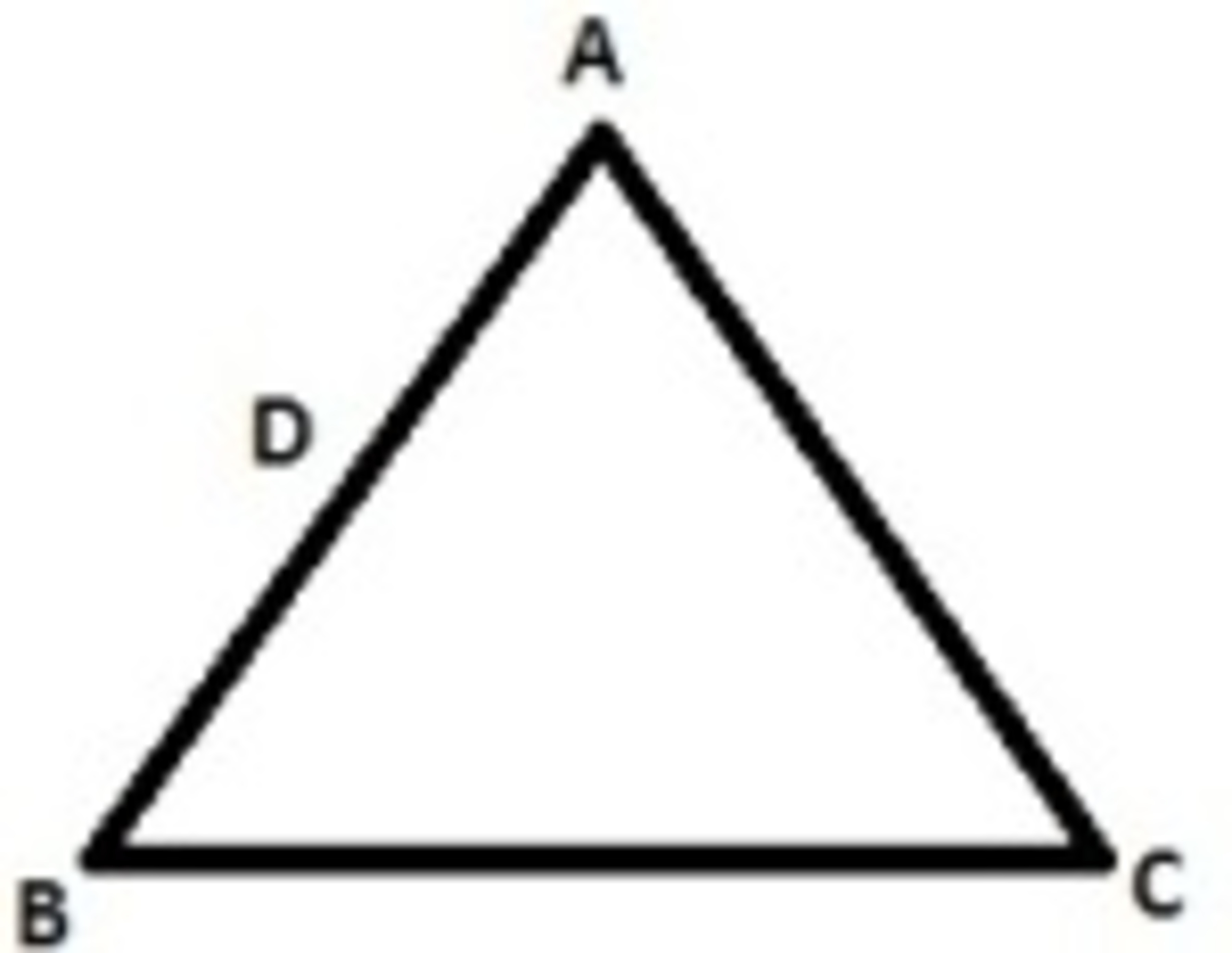
Three rods of equal lengths are joined to form an equilateral triangle
.
is the midpoint of
. The coefficient of linear expansion is
for
and
for both
and
. If
the distance
remains constant for small change in temperatures. Find the value of
.
Try my World of Physics to solve many problems like this one.
The answer is 4.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
Linear expansion due to heating is given by, L'=L(1+αΔT); where α→coefficient of linear expansion.
Before heating, DC²=AC²-AD² After hearing, (DC')²=(AC')²-(AD')² Since DC doesn't change; therefore DC=DC'. Hence, AC²-AD²=(AC')²-(AD')² AC²-AD²=AC²(1+α1ΔT)²-AD²(1+α2ΔT)² AC²-AD²=AC²[1+(α1ΔT)²+2α1ΔT]-AD²[1+(α2ΔT)²+2α2ΔT]
Since α1&α2 are small quantities therefore there square can be neglected.
Therefore, AC²-AD²=AC²(1+2α1ΔT)-AD²(1+2α2ΔT) AC²-AD²=AC²+2AC²α1ΔT-AD²-2AD²α2ΔT 0=2[AC²α1ΔT-AD²α2ΔT] AC²×α1ΔT=AD²×α2ΔT AC²×α1=AD²×α2
Since, AC=2AD Therefore, AC²×α1=4AC²×α2 viz, α1=4α2
By comparison we get n =4