Heat exchanger
A heat exchanger transfers heat from a hot water stream to a cold one and can be operated in parallel or countercurrent flow as shown below. In what configuration does the heat exchanger work most effectively and transfers the most heat?
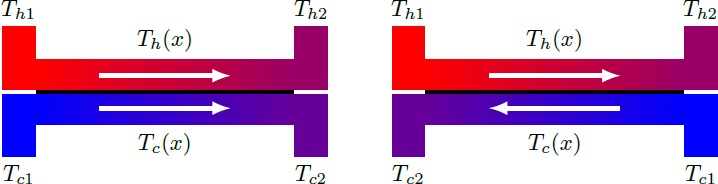
- and are the input temperatures and and are the output temperatures of the hot and cold water stream.
- The water flows have temperature profiles and with ( : length of the heat contact)
- The heat flow through a surface area of the heat contact is proportional to the local temperature gradient
- Both water streams have the same volume flow with flow velocity and pipe cross section
- A temperature change of in a volume corresponds to a heat transfer with the specify heat capacity .
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
The local heat transfer rate for both streams read c V ˙ d x d T h d x ± c V ˙ d x d T c d x = − d Q ˙ = − k w ( T h ( x ) − T c ( x ) ) d x = d Q ˙ = k w ( T h ( x ) − T c ( x ) ) d x where the plus sign and the minus sign in the latter equation respectively denoting the parallel and countercurrent flow. With the parameter λ = 2 k w / c V ˙ we get the coupled differential equations ( − T h ′ ( x ) ± T c ′ ( x ) ) = 2 λ ( 1 1 − 1 − 1 ) ( T h ( x ) ± T c ( x ) )
Countercurrent Flow
d x d T h = d x d T c applies, so that the gradient T h ( x ) − T c ( x ) = Δ T results a constant. Therefore, the functions show a linear course T h ( x ) T c ( x ) = T h 1 − a x = T c 1 + a ( L − x ) with Δ T = T h 1 − T c 1 − a L = − ( 2 / λ ) ⋅ T h ′ ( x ) = 2 a / λ , so that a T c 2 = λ 2 + L T h 1 − T c 1 = T c ( 0 ) = T c 1 + λ 2 + L L ( T h 1 − T c 1 ) in the limiting case L → ∞ we get T c 2 = T h 1 , so that the cold water stream can get as hot as the incoming hot water.
Parallel Flow
d x d T h + d x d T c = 0 applies, so that the mean temperature T m = ( T h + T c ) / 2 = const stays constant. Therefore, only the temperature difference Δ T ( x ) = T h ( x ) − T c ( x ) must be considered, so that differential equation becomes onedimensional Δ T ′ ( x ) = − λ Δ T ( x ) which is solved by Δ T ( x ) = ( T h 1 − T c 1 ) exp ( − λ x ) . The final temperature of the cold stream results to T c 2 = 2 T h 1 + T c 1 − 2 T h 1 − T c 1 e − λ L in the limit L → ∞ we get T c 2 = T m , so that cold water stream can never exceed the mean temperature.
Plotting both final temperature as function of the length L results T c 2 countercurrent ( L ) > T c 2 parallel ( L ) for all L > 0 , so that the countercurrent configuration is always more effective.