Heat it!
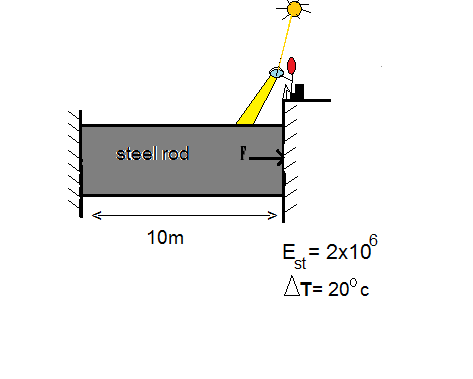 Satish varma (red one) sitting idle and playing with a magnifying glass, thought to heat the steel rod before him. He did so and after a long time he found temperature of rod increased by 20°c . cross-sectional area of rod is 15m². Help Satish find how much FORCE the rod is exerting on the rigid wall he is sitting.
Satish varma (red one) sitting idle and playing with a magnifying glass, thought to heat the steel rod before him. He did so and after a long time he found temperature of rod increased by 20°c . cross-sectional area of rod is 15m². Help Satish find how much FORCE the rod is exerting on the rigid wall he is sitting.
young's modulus =E coefficient of thermal expansion of steel α =0.000001/°c
NOTE: If u get force as integer X, then type answer as X.00 upto two decimals.
The answer is 600.00.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
We know that heating the steel will change its length:-
Δ L ⟶ change in length.
L ⟶ original length.
Change in length is given by:- Δ L = l α Δ T Plugging in values we get Δ L = 2 × 1 0 − 4 m
Also we know that:- E = A Δ L F L Rearranging:- F = L E A Δ L Plugging in values we get F = 6 0 0 . 0 0 N