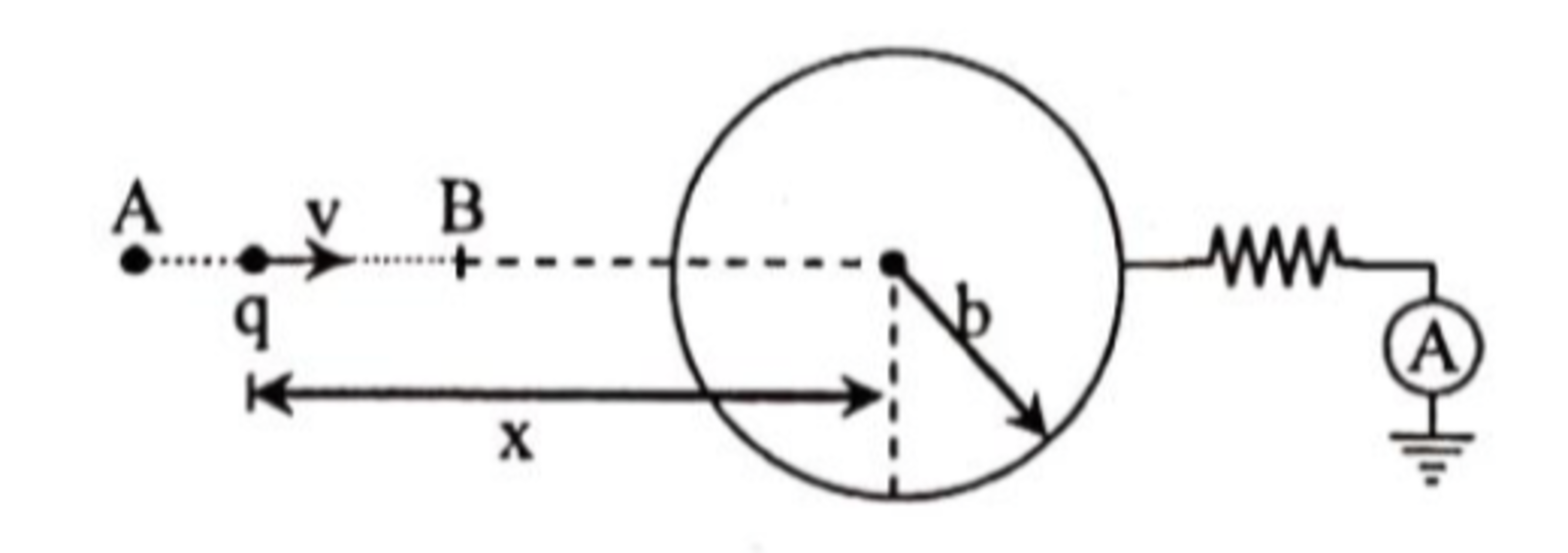
Heat produced in resistor due to charge

A charge $q$ is moving towards the centre of an earthed conducting sphere of radius $b$ with uniform velocity $v$ . Distance of two points A and B from the centre of the sphere are $3a$ and $2a$ . Conducting sphere is earthed with an ideal ammeter and a resistance $R$ in series as shown. Let, at any instant $q$ be at a distance $x$ from the centre of the sphere. The heat energy produced in the resistor till the charge moves from A to B is given as $H = \frac{\alpha q^2 b^2 v R}{\beta a^3}$ where $\alpha$ and $\beta$ are constants (fraction is in lowest form). Compute $\alpha+\beta$ .