HEAT TRANSFER IN A CONDUCTING BAR
An electric current I flows along homogenous conducting bar with length L resistivity R and thermal conductivity K . The two ends are located at X=0 and X=L In the OX axis .The temperature X=0 is T=T1 and X=L is T=T2(T1>T2) both temperatures are kept constant.
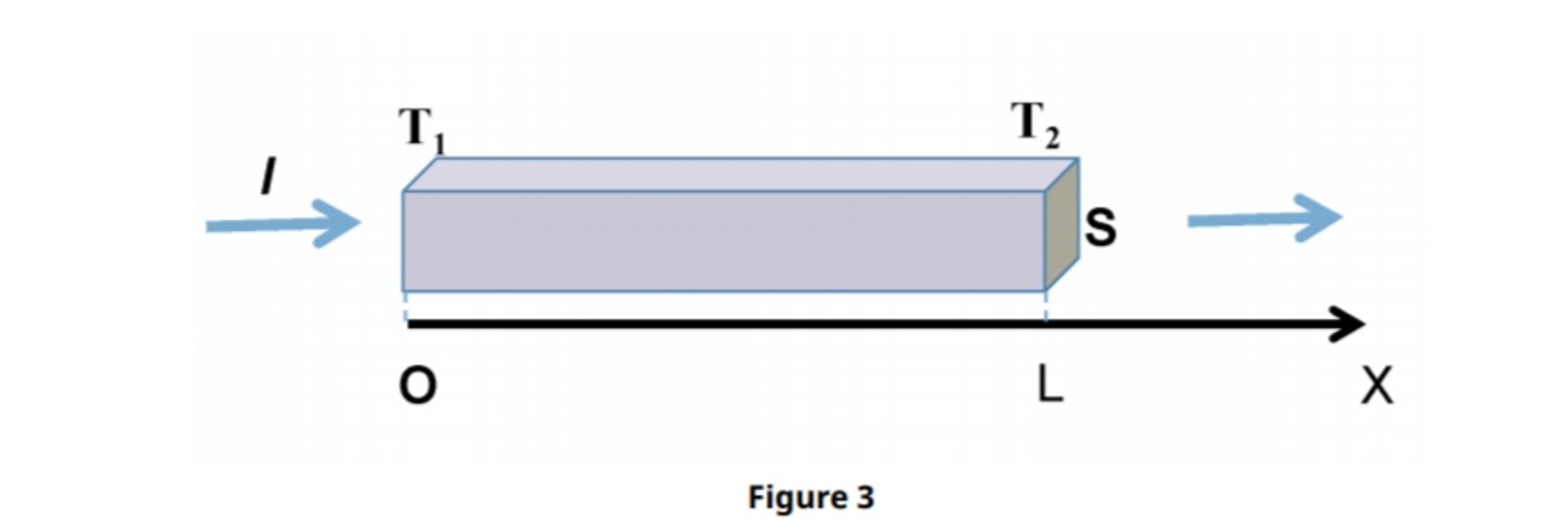 USE FOURIER LAW FOR HEAT TRANSFER AND CONSIDER ONLY JOULE LAW FOR HEAT DISSAPATION IF T1=500k , T2=200K , Crossectional area S=1 m^2 , K=109 SI unit ,L=2m,R=9.71,I=3 FIND temperature of mid point of rod
USE FOURIER LAW FOR HEAT TRANSFER AND CONSIDER ONLY JOULE LAW FOR HEAT DISSAPATION IF T1=500k , T2=200K , Crossectional area S=1 m^2 , K=109 SI unit ,L=2m,R=9.71,I=3 FIND temperature of mid point of rod
The answer is 350.4.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
Very nice problem. As current flows through the slab, the heat generated per unit time in the whole volume of the slab is:
P = S R L I 2
Therefore, the power generated per unit time, per unit volume is:
p = L S P
Now, consider an elementary volume of cross-section area S and length δ x at a distance x from the left end of the slab. The hear generated per unit time in this elementary volume is:
P v = p S δ x
Now, consider this elementary volume again. The heat per unit time flowing into the left facet of this element is Q i n and heat per unit time flowing out of this slab through its right facet is Q o u t . Applying the first law of thermodynamics for this elementary volume gives:
Q i n + P v = Q o u t … ( 1 )
Now, the rate of hear flow varies with x . Since δ x is small, one can use a Taylor series first order approximation (since δ x is small) to relate Q i n and Q o u t as such:
Q o u t = Q i n + d x d Q i n δ x ⟹ Q o u t − Q i n = d x d Q i n δ x
Now, using Fourier's law, we know that:
Q i n = − K S d x d T ⟹ d x d Q i n = − K S d x 2 d 2 T ⟹ Q o u t − Q i n = − K S d x 2 d 2 T δ x
Substituting the above result in (1) gives:
P v = − K S d x 2 d 2 T ⟹ d x 2 d 2 T = − K S 2 R I 2
We know that T ( 0 ) = T 1 and T ( L ) = T 2 .
Double integrating the above equation and substituting all boundary conditions and values gives the temperature distribution as a function of x as follows. Simplifications have been left out in this solution.
T ( x ) = − 2 1 8 0 0 8 7 3 9 x 2 − 1 0 9 0 0 1 6 2 6 2 6 1 x + 5 0 0
From the above equation, T ( L / 2 ) can be conveniently computed. The result is T ( L / 2 ) ≈ 3 5 0 . 4 K .