Heating thinks up
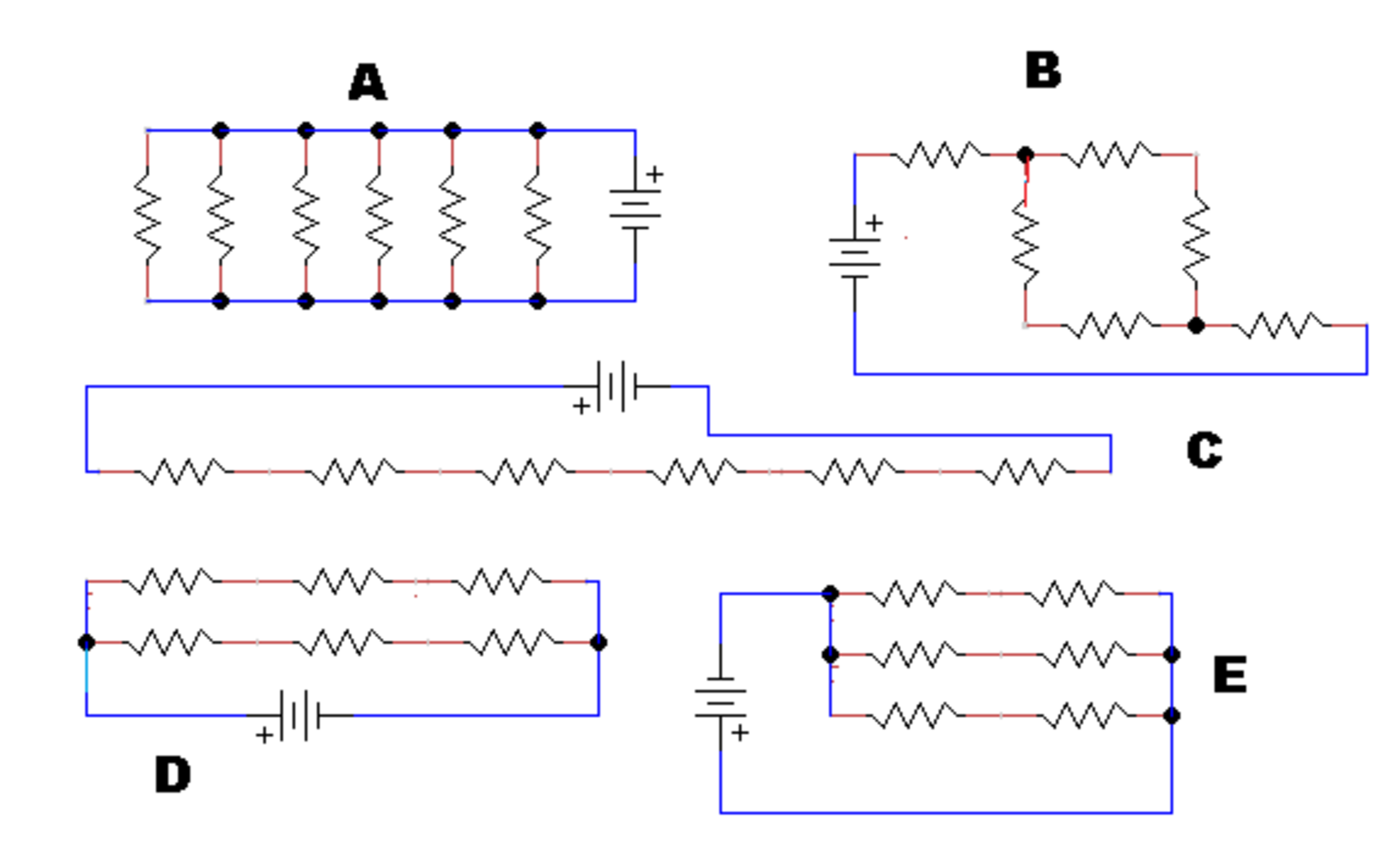
Which of the circuits shown below will produce the most heat, while not exceeding the ratings given for any of the components in the circuit?
Given;
All of the resistors are 33 ohm 0.5 watt rating.
The power supply is 12 volt DC 0.5 amp rating.
A; Schematic A
B; Schematic B
C; Schematic C
D; Schematic D
E; Schematic E
F; They all produce the same amount of heat.
G; They all exceeded at least one of the limits set by the ratings of the individual components.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
All the calculations are done using a combination of the following basic laws of electrical circuits. I am not going into detail unless it is requested.
I = R V
W = R V 2
W = V I
Schematic A Total wattage would be 26.18 watts of heat. Power consumption is far too high for the power supply and if the supply could produce the current the resistors could not dissipate the heat generated.
Schematic B Total wattage would be 1.45watts of heat. All components are within ratings.
Schematic C Total wattage would be 0.72 watts of heat. All components are within ratings.
Schematic D Total wattage would be 2.91watts of heat. All components are within ratings.
Schematic E Total wattage would be 6.55watts of heat. The total heat dissipated by any one resistor would be 1.09 watts. That is more than twice the rated wattage of the 0.5 w resistors.