Heavy slope
Let f ( x , y ) = x 2 1 + y 3 + 3 x . Let r be a line tangent to the surface determined by the graph of f at the point ( 1 , − 2 , f ( 1 , − 2 ) ) . If the angle between r and the z = 0 plane is maximum, what is its value in degrees? (Round your final answer to three decimal places).
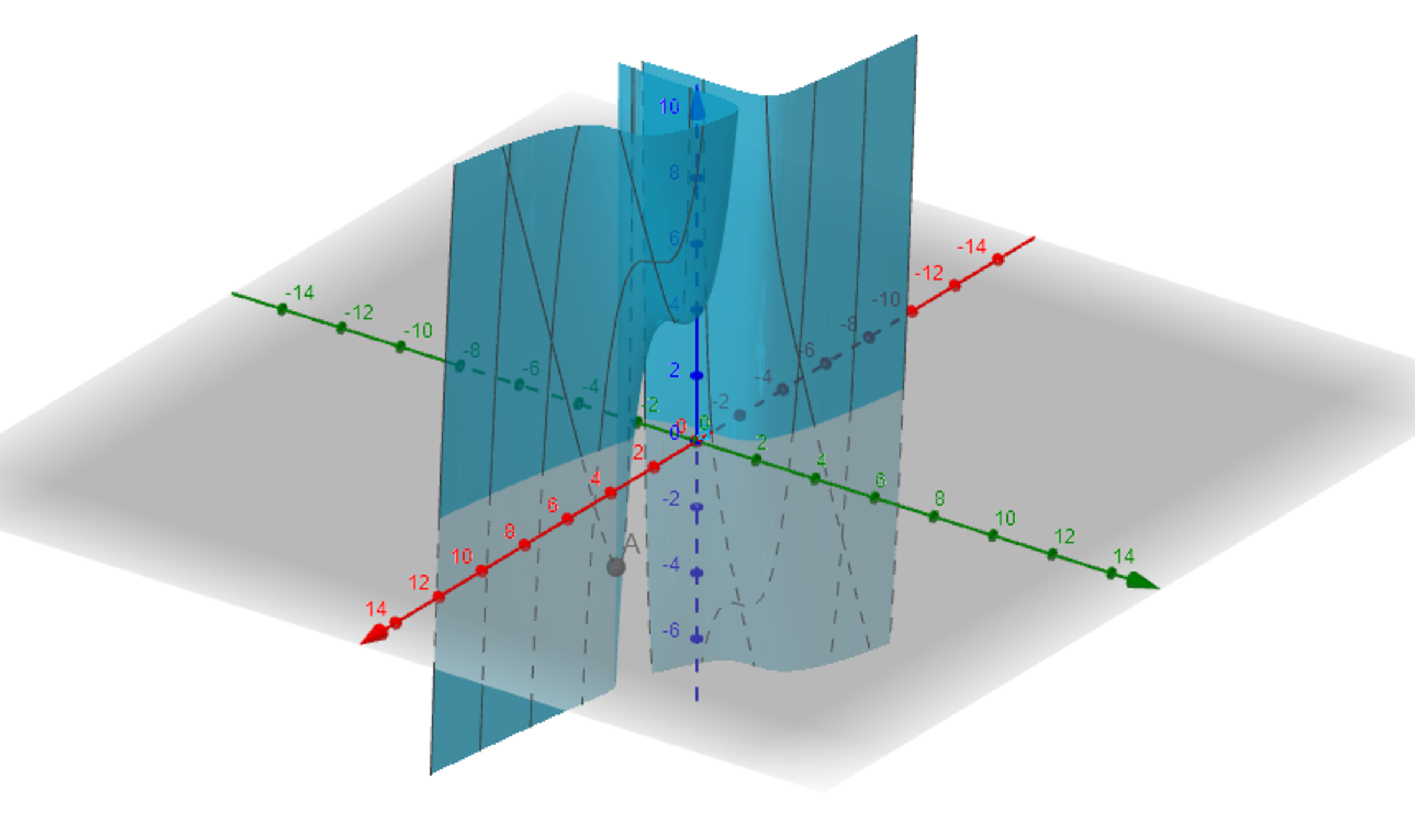
The answer is 85.253.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
5 solutions
A surface determined by the graph of a function f can be written as the implicit surface equation g ( x , y , z ) = 0 , where g ( x , y , z ) = f ( x , y ) − z . In turn, the gradient of g at ( x , y , z ) gives the components of the vector in the same direction as the vector normal to the plane which is tangent to the graph of f at this same point. Thus, ∇ g ( x , y , z ) = ( − x 3 2 + 3 , 3 y 2 , − 1 ) , ∇ g ( 1 , − 2 , f ( 1 , − 2 ) ) = ( 1 , 1 2 , − 1 ) , and the tangent plane π : ( x − 1 ) + 1 2 ( y + 2 ) − ( z + 4 ) = 0 . Setting to zero two out of the three variables in the plane equation, one finds out that the following points belong to π : ( 0 , 0 , 1 9 ) , ( 0 , − 1 2 1 9 , 0 ) and ( − 1 9 , 0 , 0 ) . Hence, ( 1 9 , 0 , 1 9 ) ∝ ( 1 , 0 , 1 ) and ( 0 , 1 2 1 9 , 1 9 ) ∝ ( 0 , 1 , 1 2 ) are direction vectors of this plane. Since the tangent line belongs to π , its direction vector must be a linear combination of the direction vectors of the plane, i.e. λ ( 1 , 0 , 1 ) + μ ( 0 , 1 , 1 2 ) = ( λ , μ , λ + 1 2 μ ) . The angle between the tangent line and the z = 0 plane must be maximized, which means that the angle between this vector and the normal to the z = 0 plane must be minimized; in turn, this means that the cosine of the angle between this vector and the normal to the z = 0 plane ( c o s α ) must be maximized. The cosine of the given angle is simply:
c o s α = ∣ ∣ ( λ , μ , λ + 1 2 μ ) ∣ ∣ ⋅ ∣ ∣ ( 0 , 0 , 1 ) ∣ ∣ ⟨ ( λ , μ , λ + 1 2 μ ) , ( 0 , 0 , 1 ) ⟩ = λ 2 + μ 2 + ( λ + 1 2 μ ) 2 λ + 1 2 μ
Taking the derivatives of this expression with respect to λ and μ , equating to zero and solving the resulting system of equations, one finds out that λ = 1 2 μ and that μ can be any real number (the other solution would give a null vector as the direction vector). Thus, the direction vector is simply μ ( 1 2 1 , 1 , 1 2 1 4 5 ) ∝ ( 1 , 1 2 , 1 4 5 ) . Therefore, c o s α = 1 4 5 ⋅ ( 1 2 + 1 2 2 + 1 4 5 2 ) − 1 / 2 ≈ 0 . 9 9 6 5 6 9 ⇒ α ≈ 4 . 7 4 7 ∘ and the sought-after angle is its complement, 8 5 . 2 5 3 ∘ .
Since z = f ( x , y ) , then g ( x , y , z ) = f ( x , y ) − z = 0 . The gradient of g is
∇ g = ( ∇ f − 1 ) = ⎝ ⎛ − 2 x − 3 + 3 3 y 2 − 1 ⎠ ⎞
At ( 1 , − 2 ) , we have
∇ g = ⎝ ⎛ 1 1 2 − 1 ⎠ ⎞
The gradient ∇ g is normal to the tangent plane to the surface g = 0 . The maximum angle between a line in this plane and the z = 0 plane is the acute angle between ∇ g and k = ( 0 , 0 , 1 ) the unit normal to the z = 0 plane. Hence, the required angle is
θ = cos − 1 ∣ ∣ ∇ g ∣ ∇ g ⋅ k ∣ = cos − 1 1 2 + 1 2 2 + 1 2 1 = cos − 1 1 4 6 1 = 8 5 . 2 5 2 7 3 ∘
The surface has normal vector ⎝ ⎛ 3 − 2 x − 2 3 y 2 − 1 ⎠ ⎞ and hence, when x = 1 , y = − 2 , we have z = f ( 1 , − 2 ) = − 4 and
n = ⎝ ⎛ 1 1 2 − 1 ⎠ ⎞ Thus the tangent plane to the surface at the point P ( 1 , − 2 , f ( 1 , − 2 ) ) has equation x + 1 2 y − z + 1 9 = 0 , which meets the z = 0 plane in the line x + 1 2 y + 1 9 = 0 , z = 0 . The closest distance from this line to the point ( 1 , − 2 ) is d = ∣ ∣ ∣ ∣ 1 + 1 2 2 1 − 2 4 + 1 9 ∣ ∣ ∣ ∣ = 1 4 5 4 and hence the largest angle that a tangent line at P makes with the z = 0 plane is tan − 1 d 4 = tan − 1 1 4 5 = 8 5 . 2 5 2 7 3 7 7 3 ∘
At ( x , y ) = ( 1 , − 2 ) , the gradient vector is found by taking the partial derivatives of f in x and y: ∇ f ( 1 , − 2 ) = ( − x 3 2 + 3 , 3 y 2 ) ∣ ∣ ∣ ∣ ( 1 , − 2 ) = ( 1 , 1 2 ) In a direction u = ( cos θ , sin θ ) , the slope at this point is u ⋅ ∇ f ( 1 , − 2 ) = cos θ + 1 2 sin θ We can rewrite this sum of trig functions as 1 2 + 1 2 2 sin ( θ + ϕ ) = 1 4 5 sin ( θ + ϕ ) for some angle ϕ . This slope attains a maximum value of 1 4 5 , hence the maximum angle between the tangent line and the z = 0 plane is arctan ( 1 4 5 ) ≈ 8 5 . 2 5 3 ∘
The gradient of f ( x , y ) = x − 2 + y 3 + 3 x is defined as the vector ∇ f = ( ∂ x ∂ f , ∂ y ∂ f ) = ( 3 − 2 x − 3 , 3 y 2 ) A gradient is just a derivative, and it determines the steepest tangent line as well as its slope. It takes the value ∇ f ( 1 , − 2 ) = ( 1 , 1 2 ) In general the slope of the graph of a 2-dim. real-valued function is given by ∣ ∇ f ( x , y ) ∣ so the angle is given by arctan ( 1 2 + 1 2 2 ) ≈ 8 5 . 2 5 3 °