Hectogon Congruency Theorem

$\begin{aligned} \text{Triangle (3)} &\implies \underbrace{\text{S}}_{1} \underbrace{\text{AS}}_{2(1)} \\ \text{Square (4)} &\implies \underbrace{\text{S}}_{1} \underbrace{\text{AS+AS}}_{2(2)} \\ \text{Pentagon (5)} &\implies \underbrace{\text{S}}_{1} \underbrace{\text{AS+AS+AS}}_{2(2)} \\ &. \\ &. \\ &. \\ \text{n-gon} &\implies \underbrace{\text{S}}_{1} \underbrace{\text{AS+AS+AS}\ldots\text{AS+AS+AS}}_{2(n-2)} \\ &. \\ &. \\ &. \\ \text{100-gon} &\implies \underbrace{\text{S}}_{1} \underbrace{\text{AS+AS+AS}\ldots\text{AS+AS+AS}}_{2(100-2)} \\ \text{100-gon} &\implies \underbrace{\text{S}}_{1} \underbrace{\text{AS+AS+AS}\ldots\text{AS+AS+AS}}_{196} \end{aligned}$

---

$\begin{aligned} \\ \text{Total elements required} &= 1+196 \\ \text{Total elements required} &= \boxed{197} \end{aligned}$

From one vertex, a $100$ -gon can be split up into $98$ triangles by $97$ diagonals. Each of the $98$ triangles needs at least $3$ pairs of angles or sides to be proved congruent, but the $97$ diagonals that are shared do not need to be counted twice, for a minimum of $3 \cdot 98 - 97 = \boxed{197}$ pairs of angles and sides.

One way to show that this is possible is to start with $\triangle ABC$ with known $\angle ABC$ and known sides $AB$ and $BC$ which can be shown congruent by SAS so that $\angle BCA$ and side $AC$ becomes known by corresponding parts, then add the next triangle $\triangle ACD$ with known $\angle BCD$ and side $CD$ which can be shown congruent by SAS again so that $\angle CDA$ and side $CD$ becomes known by corresponding parts, and so on.

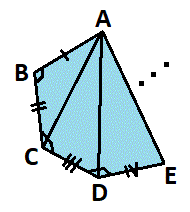
If $t_n$ is the number of angles and sides needed and $n$ is the number of sides on the polygon, then $t_3 = 3$ and $t_n = t_{n - 1} + 2$ , which can be shown by induction to have the explicit form of $t_n = 2n - 3$ .

Therefore, when $n = 100$ , $t_n = 2 \cdot 100 - 3 = \boxed{197}$ .