Height of the Book
At the back of a bookstore, there is a storeroom where multiple copies of three types of books are kept. There are copies of a novel, an autobiography, and a linear algebra textbook. Each copy of the novel is 1cm thick, each copy of the autobiography is also 1cm thick while the linear algebra textbook is 2cm thick. Determine the number of ways to stack the books into a tower -cm high.
A.
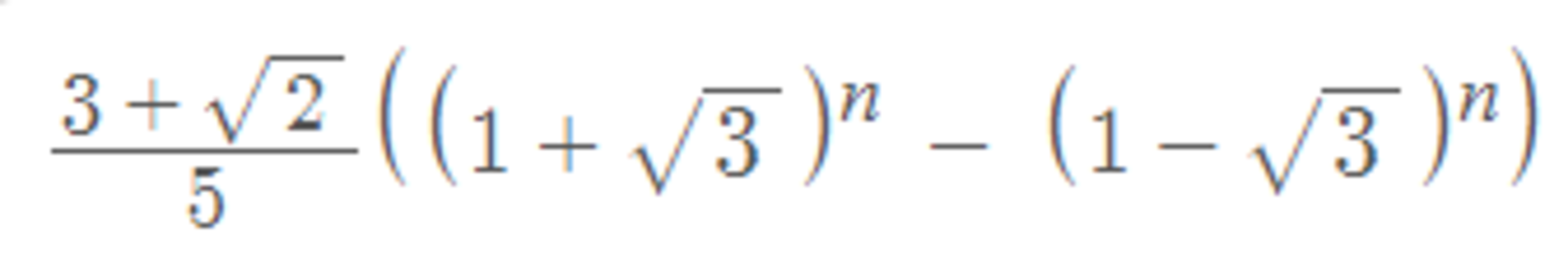 B.
B.
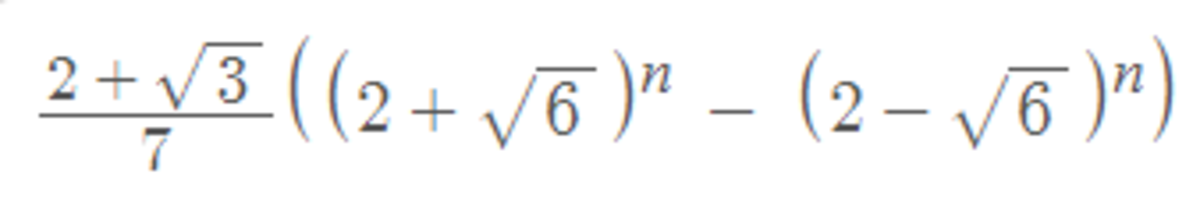 C.
C.
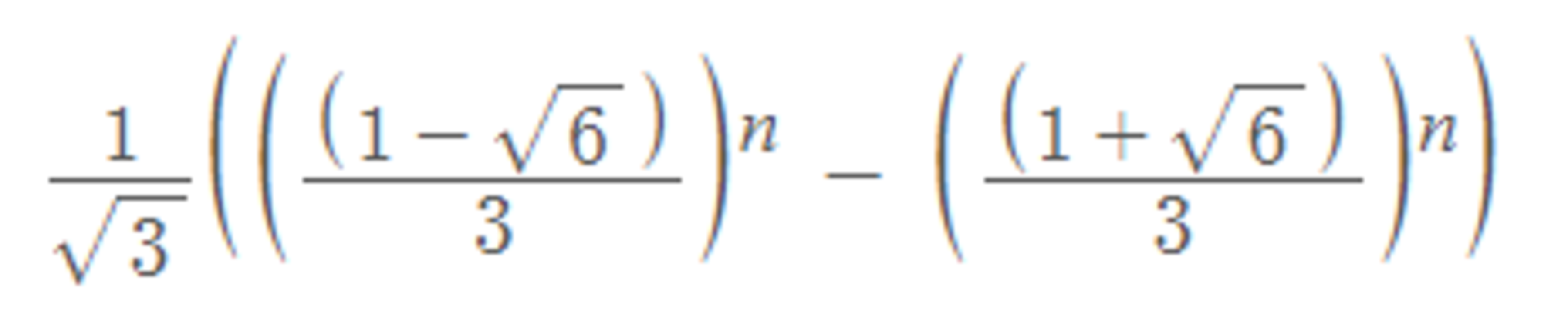 D.
D.
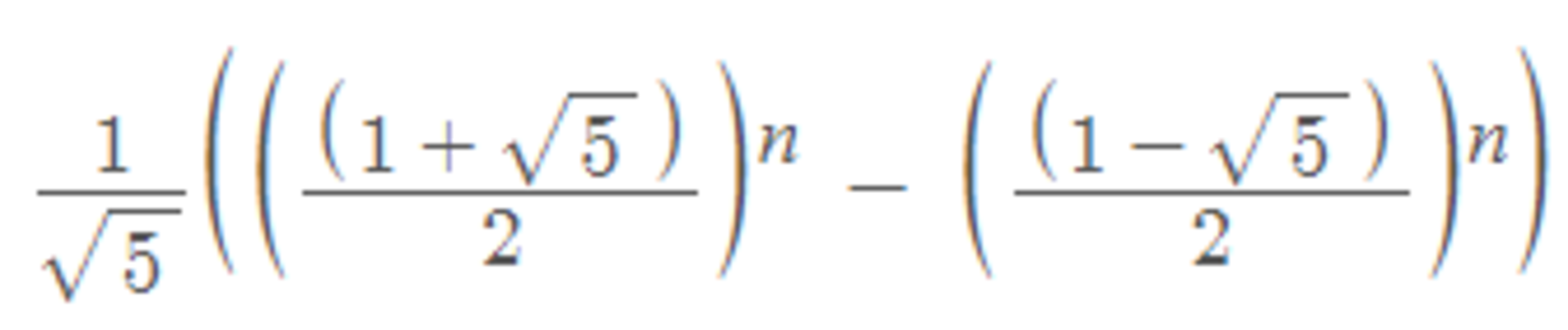 E.
E.
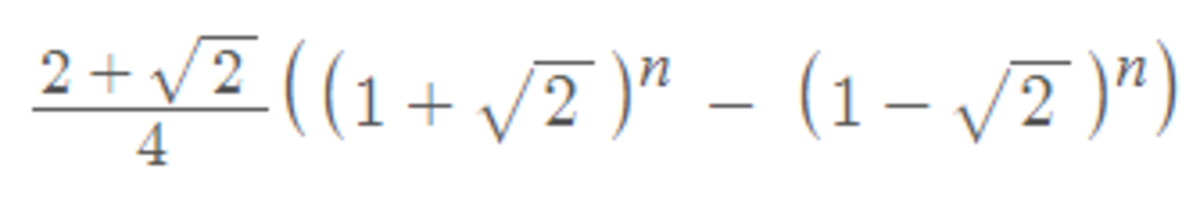
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
Let a n be the number of ways to stack the books into a tower n cm high. We consider the book at the bottom of the stack. If it is a novel, then there are a n − 1 ways to stack up the other books that will be ( n − 1 ) cm high. If the bottom book is an autobiography, then again there will be a n − 1 ways to stack up the other books that will be ( n − 1 ) cm high. If the bottom book is a linear algebra book then there are a n − 2 ways to stack up the other books that will be ( n − 2 ) cm high. So the recurrence relation is
You may wish to refer to this site for further explanation (different question, but similar)
https://medium.com/@andrew.chamberlain/the-linear-algebra-view-of-the-fibonacci-sequence-4e81f78935a3