Heist Of The Diamond
A thief, standing by the gate (down left corner), is going to steal a diamond from a guarded building with square corridors. The guard stands in the middle at the moment when the thief starts approaching the diamond. He can walk one unit per minute in the grid, and the guard also walks one unit per minute around the diamond along the red arrows. If the guard and the thief ever meet at the same coordinate, the guard will catch the thief. The thief will also be caught if he isn't back to the gate in 12 minutes.
How many different routes the thief can take to steal the diamond and then return to the gate without getting caught?
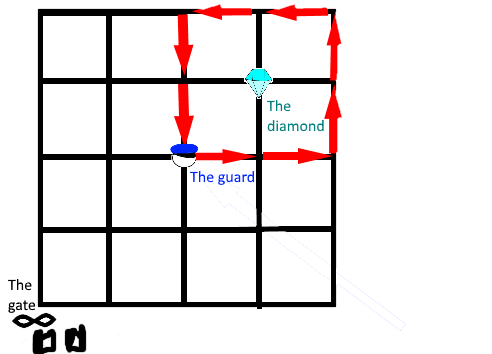
The answer is 80.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
1 solution
Relevant wiki: Rectangular Grid Walk
To reach the diamond, the thief must move 3 units north and 3 units east totally. This takes the thief 6 at least 6 minutes, and the trip back to the gate will take the same time. To be back to the gate in 12 minutes- the thief can only move north and eats when reaching the diamond, and only south and west when coming back to the gate.,The thief has 3 ! × 3 ! 6 ! = 6 4 × 5 × 6 = 2 0 different routes to the diamond, none of which will result in the thief to be arrested. The pictures below prove this, showing the positions of the diamond (cyan) and the guard (blue) and the possible positions of the thief (red) at each moment.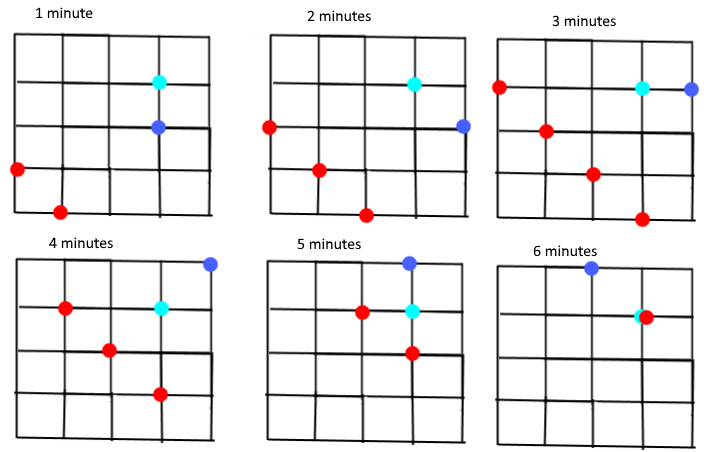
When going back to the gate, the thief can only go south for next two minutes, otherwise he/she will be caught by the guard, as the pictures below show.
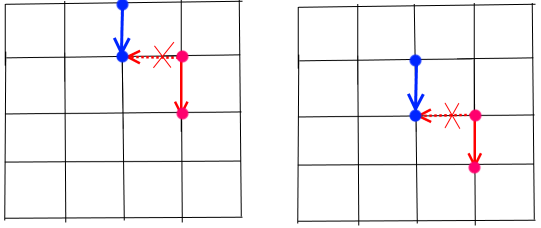Now the thief has 4 ways to go back to the gate. The total number of different routes he/she can take to steal the diamond and go back to the gate without being arrested is
4
×
2
0
=
8
0