Help UPS Solve This Impossible Routing Problem

Sue is a coordinator for UPS, and she's planning out tomorrow's route. Her next assignment is a truck in New York City, which must make 99 deliveries while driving on the rectangular grid of the city's streets.
If the coordinates the driver must reach are found in this list (measured in block lengths), which of the following is the closest to the minimum distance the truck will need to travel (in blocks)?
Image credit: Chris Hondros/Getty Images North America
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
4 solutions
The problem says that the truck must travel on a rectangular grid yet this solution calculates distances from point to point (as the crow flies.) Using the same solution but calculating distances by using simply x and y offsets I think you'd come up with 3029 (which is closer to 3100).
My code for this problem based on Manhattan distance and times the cost 2 that you can move (right or left ) , code is as follows :
import math
with open("points.txt","r") as ins:
array = []
for line in ins:
array.append(line)
temp = [] for line in array:
strr = line.strip().strip("()")
x,y = map(int,strr.split(","))
temp.append((x,y))
def distance(p1, p2):
x1 = p1[0]
y1 = p1[1]
x2 = p2[0]
y2 = p2[1]
dx = abs(x1-x2)
dy = abs(y1-y2)
return math.sqrt(2)*(dx + dy)
sum = 0 for i in temp :
minn = 10000000
for j in temp :
if i!=j and minn >= distance(i,j):
minn = distance(i,j)
sum+=minn
print sum
In this line: "return math.sqrt(2)*(dx + dy)", why are you multiplying by sqrt(2)?
Some other solvers seem to have interpreted the question differently from me. I take "while driving on the rectangular grid of the city's streets" to mean she can only drive parallel to the coordinate axes. I've also assumed she can start anywhere and finish anywhere.
The minimum spanning tree covers distance 2379, so that's a lower bound (since her route goes to every vertex).
We can get a distance of 2992 by choosing the closest point not yet visited.
The best route I found covers a distance of 2792. I find a route using the algorithm above, and then try to improve it by switching points around.
So we know that the minimum distance is somewhere between 2379 and 2792.
Here's the Matlab code I used:
coords=importdata("UPScoordinates.txt");
X=zeros(100,2);
for i=1:100
L=length(coords{i});
for j=1:L
if coords{i}(j)==",", break; end
end
X(i,:)=[str2double(coords{i}(2:j-1)) str2double(coords{i}(j+1:L-1))];
end
%setting up takes ~0.2s
tic
k=1;
dists=zeros(100);
for i=1:100
for j=1:i-1
pairs0(k,:)=[i,j];
k=k+1;
dists(i,j)=abs(X(i,1)-X(j,1))+abs(X(i,2)-X(j,2));
end
end
dists=dists+dists';
minDist=10000;
for n=1:400
perm(1)=randi(100);
possNext=[1:100];
possNext(perm(1))=[];
for i=2:100
[~,indx]=min(dists(possNext,perm(i-1)));
perm(i)=possNext(indx);
possNext(indx)=possNext(101-i);
possNext(101-i)=[];
end
t=0;
pairs=pairs0(randperm(4950),:);
i=1;
while t<4950
for j=1:6
K=1+randi(19); %Switching 2 groups of size K
a=randi(min(70,97-2*K));
b=a+K+1+randi(98-a-2*K);
swapCost= dists(perm(a),perm(b+1))+dists(perm(b+K),perm(a+K+1))-dists(perm(a), perm(a+1))-dists(perm(a+K),perm(a+K+1));
swapCost=swapCost+dists(perm(b),perm(a+1))+dists(perm(a+K),perm(b+K+1))-dists(perm(b), perm(b+1))-dists(perm(b+K),perm(b+K+1));
if swapCost<0
y=perm(a+1:a+K);
perm(a+1:a+K)=perm(b+1:b+K);
perm(b+1:b+K)=y;
t=0;
end
end
a=pairs(i,1); b=pairs(i,2);
swapCost=0;
if a<100
swapCost=swapCost+dists(perm(b),perm(a+1))-dists(perm(a),perm(a+1));
end
if b>1
swapCost=swapCost+dists(perm(a),perm(b-1))-dists(perm(b),perm(b-1));
end
if a>b+1
swapCost=swapCost+dists(perm(a),perm(b+1))+dists(perm(b),perm(a-1))-dists(perm(b),perm(b+1))-dists(perm(a),perm(a-1));
end
if swapCost<0
x=perm(a);
perm(a)=perm(b);
perm(b)=x;
t=0;
else
t=t+1;
end
i=i+1;
if i>4950, i=1; end % > vs ==
end
d=0;
for i=1:99
d=d+dists(perm(i),perm(i+1));
end
ds(n)=d;
if d<minDist
minDist=d;
bestRoute=X(perm,:);
end
end
toc
And here's the best route I found: 81 134 65 139 33 149 28 131 21 120 15 130 -6 130 -4 133 3 153 -10 155 -30 181 -49 184 -73 186 -84 182 -94 177 -62 152 -46 88 -58 70 -63 60 -73 33 -72 21 -71 7 -47 18 -21 19 -16 19 -14 7 -26 -2 -31 -27 -25 -43 -4 -40 -1 -25 2 -14 12 5 21 8 42 2 40 -19 37 -19 18 -37 19 -83 18 -90 4 -70 -24 -70 -32 -97 -52 -104 -63 -96 -67 -99 -74 -113 -97 -116 -100 -119 -92 -151 -67 -159 -82 -183 -93 -197 -70 -193 -49 -186 -42 -188 -35 -134 -13 -134 -17 -129 4 -119 -11 -156 13 -163 12 -178 30 -180 49 -198 35 -167 43 -145 55 -149 72 -156 86 -157 80 -153 79 -146 78 -130 83 -121 69 -112 36 -108 43 -79 74 -74 75 -20 89 -17 89 -3 86 21 71 43 52 28 37 46 41 62 41 97 47 90 96 74 56 51 -4 63 -26 73 -98 73 -99 87 -95 -4 -93 -26 -100 -50 -72 -41 -58 -65 -50 -59
I took a shot at the actual path using Solver in Excel. My best answer is 3096. Path for this answer is below ( If you would like the solver solution drop a request here with mention of the UPS routing problem and I shall email it to you.)
-72 -41
-100 -50
-93 -26
-95 -4
-71 7
-47 18
-21 19
-72 21
-73 33
-63 60
-58 70
-98 73
-99 87
-94 177
-84 182
-73 186
-49 184
-30 181
-62 152
-46 88
-26 73
-4 63
47 90
41 97
21 120
28 131
15 130
-6 130
-4 133
-10 155
3 153
33 149
65 139
81 134
96 74
41 62
37 46
56 51
71 43
86 21
89 -3
89 -17
40 -19
37 -19
75 -20
74 -74
43 -79
36 -108
4 -119
-17 -129
-13 -134
-11 -156
13 -163
12 -178
30 -180
35 -167
43 -145
55 -149
80 -153
79 -146
78 -130
69 -112
83 -121
86 -157
72 -156
49 -198
-42 -188
-49 -186
-70 -193
-93 -197
-82 -183
-67 -159
-92 -151
-100 -119
-97 -116
-74 -113
-67 -99
-63 -96
-52 -104
-35 -134
-32 -97
-24 -70
-25 -43
-4 -40
4 -70
19 -83
18 -90
18 -37
-1 -25
2 -14
42 2
52 28
21 8
12 5
-14 7
-16 19
-26 -2
-31 -27
-50 -59
-58 -65
I found 2814 blocks, if we have to find a loop (going back to start). If not, it's possible to do it with less than 2800 blocks.
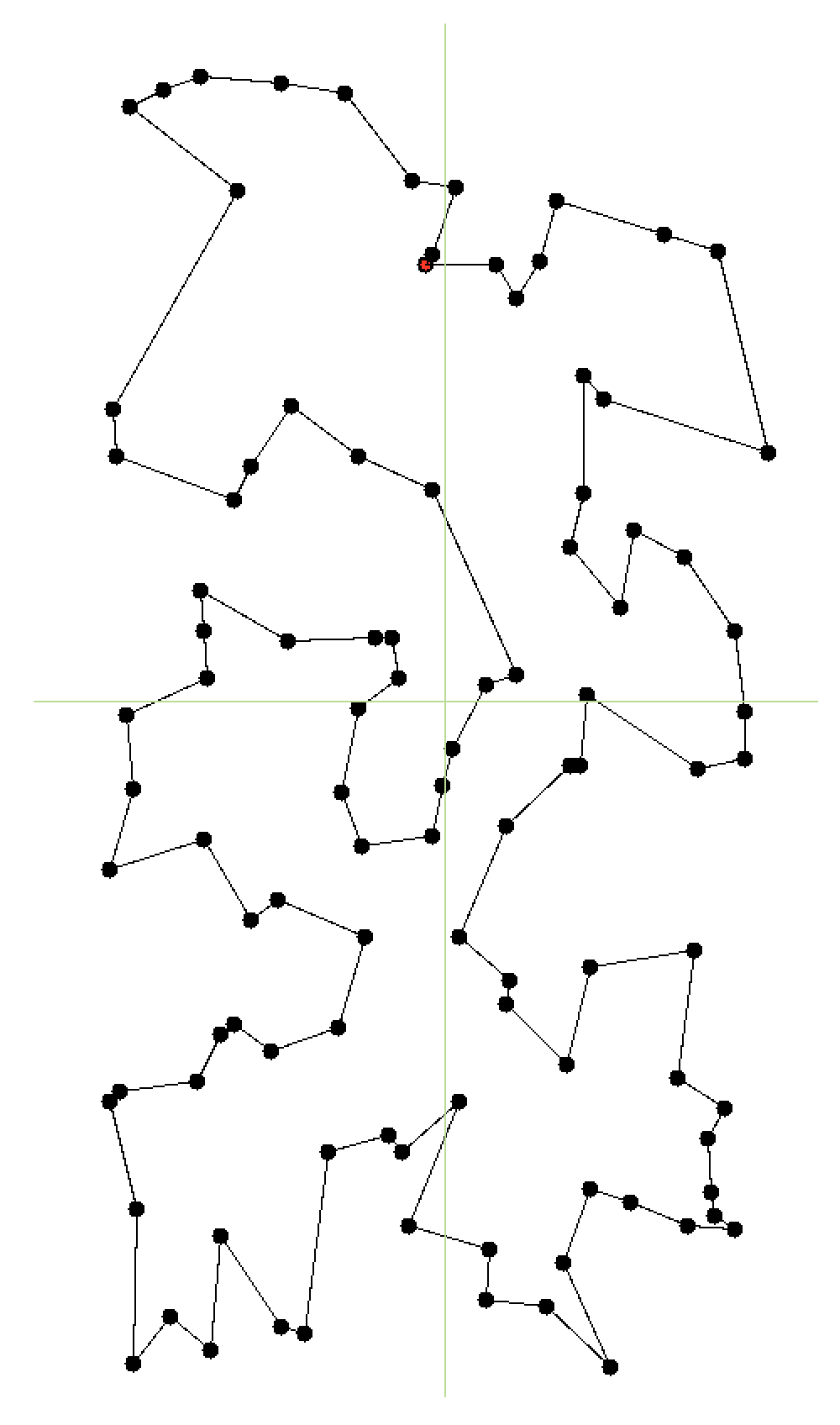 Graph with 2814 blocks
Graph with 2814 blocks
(-6,130)
(15,130)
(21,120)
(28,131)
(33,149)
(65,139)
(81,134)
(96,74)
(47,90)
(41,97)
(41,62)
(37,46)
(52,28)
(56,51)
(71,43)
(86,21)
(89,-3)
(89,-17)
(75,-20)
(42,2)
(40,-19)
(37,-19)
(18,-37)
(4,-70)
(19,-83)
(18,-90)
(36,-108)
(43,-79)
(74,-74)
(69,-112)
(83,-121)
(78,-130)
(79,-146)
(80,-153)
(86,-157)
(72,-156)
(55,-149)
(43,-145)
(35,-167)
(49,-198)
(30,-180)
(12,-178)
(13,-163)
(-11,-156)
(4,-119)
(-13,-134)
(-17,-129)
(-35,-134)
(-42,-188)
(-49,-186)
(-67,-159)
(-70,-193)
(-82,-183)
(-93,-197)
(-92,-151)
(-100,-119)
(-97,-116)
(-74,-113)
(-67,-99)
(-63,-96)
(-52,-104)
(-32,-97)
(-24,-70)
(-50,-59)
(-58,-65)
(-72,-41)
(-100,-50)
(-93,-26)
(-95,-4)
(-71,7)
(-72,21)
(-73,33)
(-47,18)
(-21,19)
(-16,19)
(-14,7)
(-26,-2)
(-31,-27)
(-25,-43)
(-4,-40)
(-1,-25)
(2,-14)
(12,5)
(21,8)
(-4,63)
(-26,73)
(-46,88)
(-58,70)
(-63,60)
(-98,73)
(-99,87)
(-62,152)
(-94,177)
(-84,182)
(-73,186)
(-49,184)
(-30,181)
(-10,155)
(3,153)
(-4,133)
(-6,130)
I made a program using c++ which finds the shortest distance from the starting point to the next point it must travel to, i.e. it finds shortest distance from ( 0 , 0 ) among the given set of points. Then it finds the shortest distance from that point among the other points.
I got 2 7 5 2 as the answer.
Here's the code: