Heptagons? I can't even draw those!
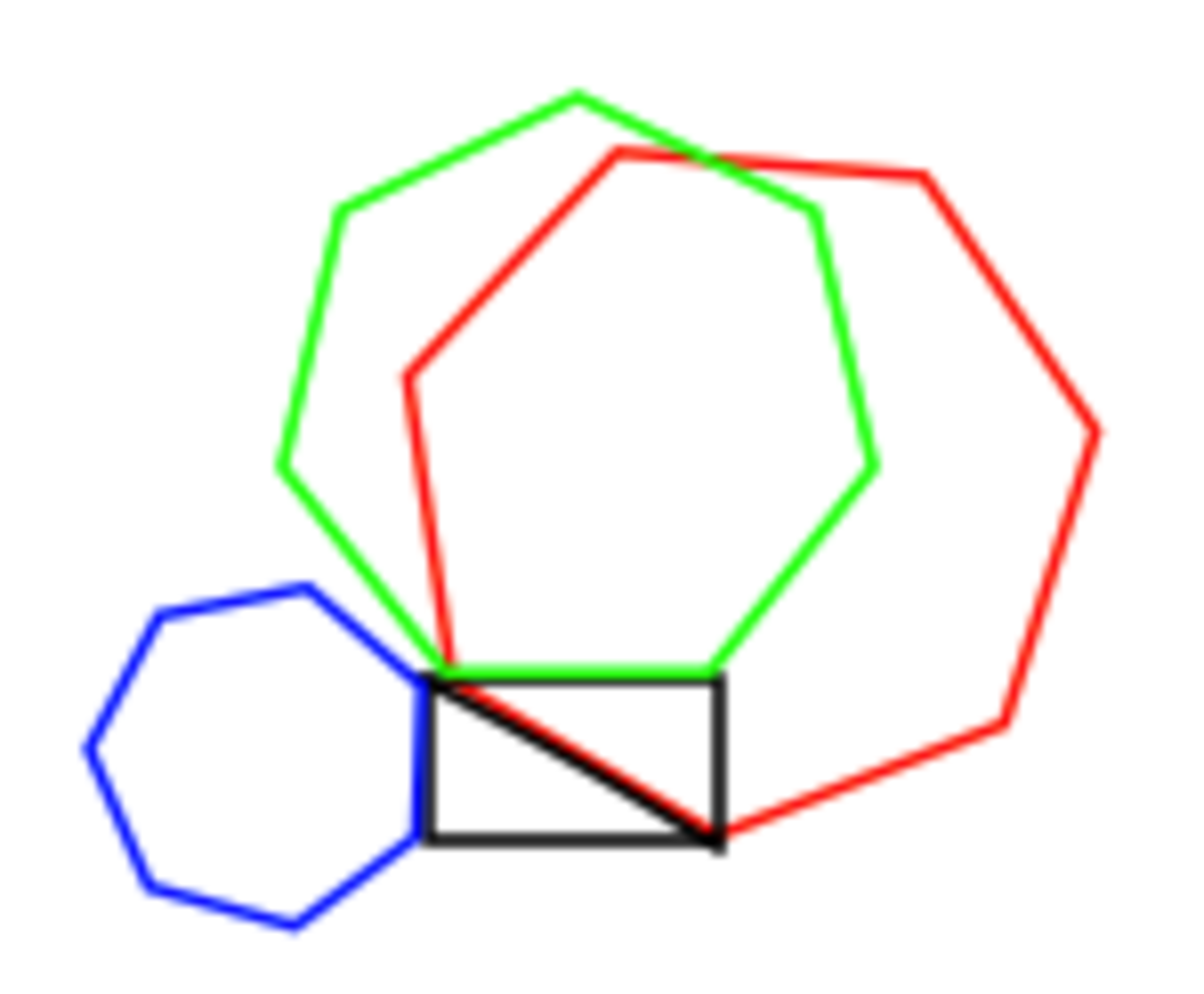
On the sides and diagonal of a rectangle, Andrew creates regular heptagons (or septagons) with their side lengths matching the length of the segment they are on. What is the relationship between the areas?
Note: Let represent the area, represent the area, and represent the area.
For those who are colorblind: the red area is the one on the diagonal, the green is the one on the long side, and the blue is the one on the short side.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
Relevant wiki: Pythagorean Theorem
The area of a heptagon is 4 7 × x 2 cot ( 7 1 8 0 ° ) , given a side length x . Call the short side of the rectangle a , the long side b , and the diagonal c . Thus, our three equations for the areas of the heptagons are
4 7 × a 2 cot ( 7 1 8 0 ° ) , 4 7 × b 2 cot ( 7 1 8 0 ° ) , 4 7 × c 2 cot ( 7 1 8 0 ° ) .
We know due to the pythagorean theorem that a 2 + b 2 = c 2 . Also k ( a 2 ) + k ( b 2 ) = k ( c 2 ) because of the distributive property. In this case, k = 4 7 × cot ( 7 1 8 0 ° ) . Thus, we know that 4 7 × a 2 cot ( 7 1 8 0 ° ) = 4 7 × b 2 cot ( 7 1 8 0 ° ) + 4 7 × c 2 cot ( 7 1 8 0 ° ) . Then, R = G + B .
Note: It is not necessary to know the formula for the area of a heptagon to solve this problem. All that is needed is that the formula has an x 2 in it somewhere, and the rest is constant.