Heptaparaparshinokh
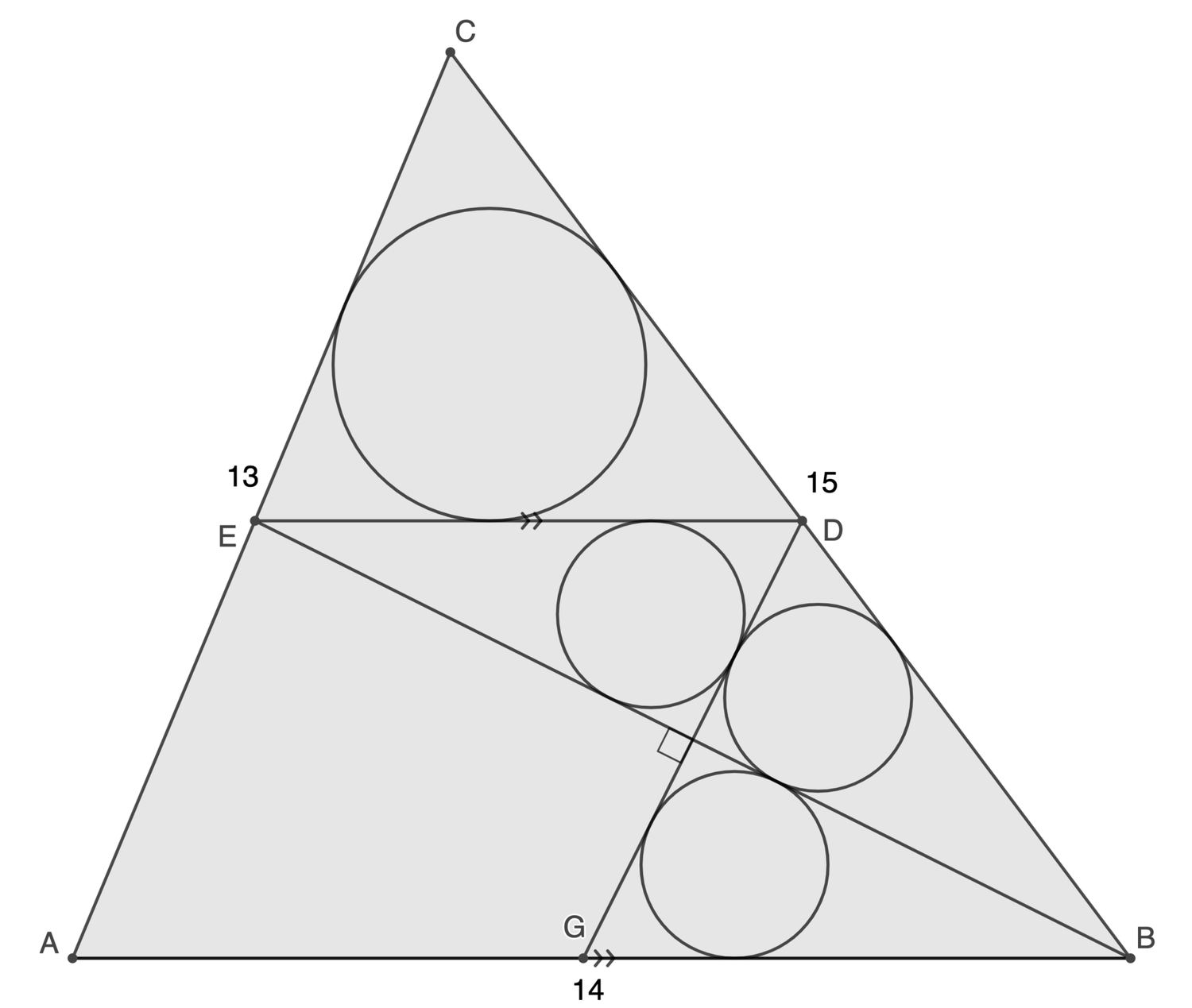
is a - - triangle. and . If the three small circles are congruent and the radius of the large circle is , where and are coprime positive integers, submit .
The answer is 89.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
Let E B and D G intersects at H . We note that the four triangles E D H , D B H , H B G , and E H G are congruent and E G ∥ D B . Also that △ E D C , △ A G E , and △ A B C are similar.
Let D B = E G = x . Then A G E G = A B B C , ⟹ 1 4 − x x = 1 4 1 5 ⟹ x = 2 9 1 4 × 1 5 . Let the radius of the large circle be r and the inradius of △ A B C be R . Then
R r ⟹ r = B C C D = 1 5 1 5 − x = 2 9 1 5 = 2 9 1 5 R = 2 9 1 5 × s A = 2 9 1 5 × 2 1 ( 1 3 + 1 4 + 1 5 ) 2 1 × 1 4 × 1 2 = 2 9 6 0
Therefore p + q = 6 0 + 2 9 = 8 9 .