Her name is Cheryl.

Computer Science Level 3

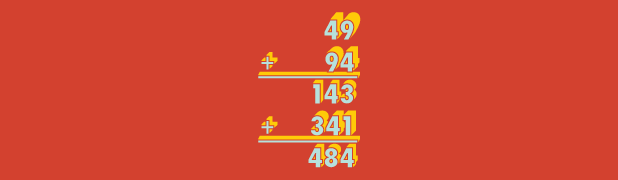I have an integer (in decimal representation) such that if I reverse its digits and add them up, I will get a new integer. I repeat this process until the resulting integer is a palindrome. We will denote an integer as a near-symmetric number if after twenty-five iterations, the resulting integer is still not a palindrome. What is the smallest positive near-symmetric number?

Details and assumptions

A palindrome is a number that remains the same when its digits are reversed.
As an explicit example, consider the integer to be $49$ . The resulting number will be $49 + 94 = 143$ . Repeat: $143 + 341 = 484$ , which is a palindrome (after $2 < 25$ iterations). Thus $49$ is not a near-symmetric number.

The answer is 196.

6 solutions

Discussions for this problem are now closed

Mark Mottian
Apr 14, 2014

This is the Python programme I wrote to find the solution:

num = 0
flag = 0

def palindrome(n):  #This function determines if a number is a palindrome
    if n == int(str(n) [::-1]):
        return True
    else:
        return False

while flag <> 1: 
    count = 0
    num = num + 1
    testnum = num

#This finds the number of times the variable 'testnum' must add itself to its digits   
#reversed before the result is a palindrome

    while palindrome(testnum) == False: 
        testnum = testnum + int(str(testnum)[::-1])
        count = count + 1

        if count == 25: 
            print num
            flag = 1    #This stops the first while loop
            break

The programme returns 196 as the answer.

Can anyone write a function that reverses the digits of an integer without using strings?

Thaddeus Abiy - 7 years, 1 month ago

Hi Thaddeus! I've written this function, which reverses the digits of a number without strings, in Python.

def reverseDigits(x):
    digits = []
    count = 0
    num = 0

#this gets each individual digit of 'x' in reverse order and stores it in an array
    while x > 0:    
        n = x % 10
        digits.append(n)
        x = x/10

#determine the amount of digits in the integer
    for element in digits:    
        count = count + 1

    for element in digits:    #calculate the number reversed
        count = count - 1
        num = num + (element*(10**count))

    return num

Reply and tell me what you think.

Mark Mottian - 7 years, 1 month ago

Nice!How does the speed of this compare to converting to a string,reversing and rehanging to int?

Thaddeus Abiy - 7 years, 1 month ago

Its simple if we know the number of digits. For a four digit integer:

Let n be the integer.

int a = Math.floor(n/1000); n-=(a 1000); int b = Math.floor(n/100); n-=(b 100); int c = Math.floor(n/10); n-=(c 10); int d = n; int rev_of_n = (d 1000) + (c 100) + (b 10) + a; return rev of n;

rev of n would be the reverse of n.

If we don't know the number of digits it wouldn't be impossible but it wouldn't be as simple as that either. We would probably have to find the number of digits. We could convert it to string and use str.length() or we can compare it to 10, 100, 1000, 10000, etc. and determine its length. After finding the length, the part of getting the seperate integers would be the same but the second part can be changed to :

int l = 4 //Here I've taken length/l as 4 because I've obtained for digits from the number(a,b,c,d) int x= x//This would be the actual length of the number, which we've found using one of the methods mentioned above. int rev of n = Math.floor((d Math.pow(10,x-1)) + (c * Math.pow(10, x-2)) + (b Math.pow(10, x-3)) +(a*Math.pow(10,x-4)));

Aditya Sriram - 7 years, 1 month ago

I am aware of such methods but they fail for larger integers.

Thaddeus Abiy - 7 years, 1 month ago

@Pi Han Goh Why is it "near symmetric" if it fails to become a palindrome (which is symmetric)?

Also, what does Cheryl have to do with this problem?

Calvin Lin Staff - 7 years, 1 month ago

Search for "Lychrel number" on google.The person who hypothesized the existence of these numbers' girlfriend's name was Cheryl so he anagrammed it(though there's an extra "l")

Tan Li Xuan - 7 years, 1 month ago

Oh haha. I heard of these numbers before, but didn't know they had a name. Thanks!

Calvin Lin Staff - 7 years, 1 month ago

Its not symmetric but it appears to be after quite a number of iterations. Cheryl is an anagram of Lerhcyl.

Pi Han Goh - 7 years, 1 month ago

near-anagram

Pi Han Goh - 7 years, 1 month ago

Eric Zhang
Apr 21, 2014

This is my Python 2 solution (actually did this in the shell, but I transferred it to a program):

def reverse_sum(n): # find sum of n and n reversed
    return int(''.join(reversed(str(n)))) + n

def is_palindrome(n): # check if n is a palindrome
    return str(n) == ''.join(reversed(str(n)))

for i in xrange(1,501): # loop through a good amount of values; can increase if no solution found
    counter = 1
    x = i
    while not is_palindrome(x) and counter < 26: # repeat the sum while it's not a palindrome
        x = reverse_sum(x)
        counter += 1
    if counter == 26: # if counter is at max then it's not a palindrome
        print "Succes! " + str(n) + " = " + str(x)
        break
    print str(n) + ": " + str(x)

Sample output: http://pastebin.com/qRSuxceQ

I see some interesting things going on with 89 and 98.

Good way for reverse sum and is palindrome, you could loop through a natural number generator:

def natural_numbers():
    """make a stream to generate natural numbers"""
    i = 1
    while True:
        yield i
        i = i + 1

shi zhz - 7 years, 1 month ago

Well, I wanted it to stop if there wasn't any found at 500, because if there wasn't, I probably would need to modify my program a bit to make it search through larger numbers more efficiently.

Thanks though.

Eric Zhang - 7 years, 1 month ago

Sabarinath M S
May 16, 2014

New to java...

public class Nearsymmtry {

public static void main(String[] args) {
    // TODO Auto-generated method stub

    int i,l;
    long m,n;

    for(l=1;;l++)
    {

      for(m=l,n=Reversa(l),i=0;i<25;i++)
      {
          m=m+n;
          n=Reversa(m);
          if(m==n)break;
      }


    if(i==25)break;

    }

    System.out.println("Least Near symmetric no. is " + l);
}

private static long Reversa(long m) {
    // TODO Auto-generated method stub

    long n,O;
    for(O=m,n=0;O>0;O/=10)
        n=(10*n)+(O%10);

    return n;
}

} //Output: Least Near symmetric no. is 196

Siddharth Singh
May 14, 2014

This is my solution to the problem using Java. It took 0.001116411 seconds to give the output.

  public class Cheryl
{

 public long reverse(long sub)
 {
      long r,rev=0l;
   while(sub>0)
    {
      r=sub%10;
      rev=rev*10+r;
      sub=sub/10;
      }
      return rev;
    }
     public boolean isPallindrome(long n)
{
    long rev=reverse(n);
    if(rev==n)
    return true;
    return false;
}
public boolean isNear_Symmetric(int n)
{
    long a=10l,c=0l;
    boolean t=true;

    while(true)
    {
        if(t==true)
        {
            a=n+reverse(n);
            t=false;
        }

        else
        a=a+reverse(a);

        if(c>=25)
        return true;
        if(isPallindrome(a)&&c!=25)
        return false;
        else
        c++;
    }
}


    public static void main()
    {
    double startTime=System.nanoTime();
    int i;
    Cheryl obj=new Cheryl();
    for(i=10;;i++)
    {
        if(obj.isNear_Symmetric(i))
        {
            System.out.println("Answer "+i);
            break;
        }
    }
    double endTime=System.nanoTime();
    System.out.println("Took "+(endTime - startTime)/1000000000 + " s");
}
}

Sanjay Kamath
Apr 17, 2014

Here is my solution in C#

Here is the recursive function : 

private void GeneratePalindromeTotals(double num1, double num2, ref int nc, ref ArrayList ar)
    {
        //Her name is Cheryl

        ar = new ArrayList();

        string rvnum1 = String.Empty;
        string rvnum2 = String.Empty;

        double rnum = 0;
        string snum2 = String.Empty;

        string snum1 = num1.ToString();

        int lnum1 = snum1.Length;

        for (int u = lnum1 - 1; u >= 0; u--)
        {
            snum2 += snum1.Substring(u, 1);
        }

        num2 = double.Parse(snum2);

        rnum = num1 + num2;


        rvnum1 += rnum.ToString();


        for (int rv = rnum.ToString().Length - 1; rv >= 0; rv--)
        {
            rvnum2 += rvnum1.ToString().Substring(rv, 1).ToString();
        }

        if (!(rvnum1.Equals(rvnum2)))
        {
            File.AppendAllText(@"C:\WriteLines.txt", "No is : " + num1.ToString() + " , Diff : rvnum1 = " + rvnum1 + " ," + "rvnum2 = " + rvnum2 + " ,nc = " + nc.ToString() + Environment.NewLine);


            nc += 1;
            if (nc.Equals(26)) return;
            GeneratePalindromeTotals(double.Parse(rvnum1), double.Parse(rvnum2), ref nc, ref ar);

            //if (nc > 25)
            //{
            //    ar.Add(num1.ToString());
            //}

            rvnum1 = String.Empty;
            rvnum2 = String.Empty;
            snum2 = String.Empty;

        }
        else
        {
            File.AppendAllText(@"C:\WriteLines.txt", "No is : " + num1.ToString() + " , Same : rvnum1 = " + rvnum1 + " ," + "rvnum2 = " + rvnum2 + " ,nc = " + nc.ToString() + Environment.NewLine);
            nc = 0;
            return;
        }
    }

   Here is the calling subroutine :

         int a_nc = 0;
        ArrayList a_ar = new ArrayList();

        for (double a_no1 = 1; a_no1 < 200; a_no1++)
        {
            Application.DoEvents();
            lblCounter.Text = a_no1.ToString();

            GeneratePalindromeTotals(a_no1, a_no1, ref a_nc, ref a_ar);
            if (a_nc.Equals(26)) { MessageBox.Show(a_no1.ToString()); break; }
        }

Aditya Sriram
Apr 14, 2014

I wrote a Java program for this. It's quite long :P

public class Near_Symmetric {

public static boolean isPalindrome(String str)
{
    StringBuffer sb = new StringBuffer(str);
    StringBuffer rev = sb.reverse();
    String str2 = rev.toString();
    if(str.equals(str2))
        return true;
    else
        return false;
}
public static boolean isPalindrome(long n)
{
    String str = Long.toString(n);
    return isPalindrome(str);
}
public static long rev(long n)
{
    String st = Long.toString(n);
    StringBuffer sb = new StringBuffer(st);
    StringBuffer rev = sb.reverse();
    String rev1=rev.toString();
    return Long.parseLong(rev1);
}
public static long val(long n)
{
    long c=0, sum=0; //btw 'c' is for 'count'
    for(long i=0;i<26;i++)
    {
        sum = n + rev(n);
        c++;
        if(isPalindrome(sum))
        {
            break;
        }
        else
            n = sum;
    }
    return c;
}
public static void main(String []args)
{
    long k=1, i=1;
    while(k==1)
    {
        long v = val(i);
        if(v>=25)
            break;
        else
            i++;    
    }
    System.out.println("Smallest near symmetric number is "+i);
}

}

And it returned 196.

couldn't find my mistake.

import java.io. ; class near_symmetric { boolean palindrome(int n) { int m=reverse(n); if(m==n) return true; else return false; } int reverse(int n) { int x=n; int s=0; while(x!=0) { int d=x%10; s=s 10+d; x=x/10; } return s; } int adding(int n) { int x=reverse(n); int sum=n+x; return sum; } void nearsymmetric() { for(int i=10;;i++) { int count=1; int x=i; while(count<=25) { int sum=adding(x); boolean judge=palindrome(sum); if(judge==true) break; else { x=sum; count++; } } if(count==26) { System.out.println(i); break; } } } }

Sagnik Ghosh - 7 years, 1 month ago

paste the program....in a note pad........and plzz help me out guys......

Sagnik Ghosh - 7 years, 1 month ago

Try changing s=s10+d to s=s*10+d and change count==26 to count>25. See if that solves the problem.

Aditya Sriram - 7 years, 1 month ago

Her name is Cheryl.

The answer is 196.

6 solutions

Discussions for this problem are now closed

0 pending reports