Here's a basic ellipse

Geometry Level 1

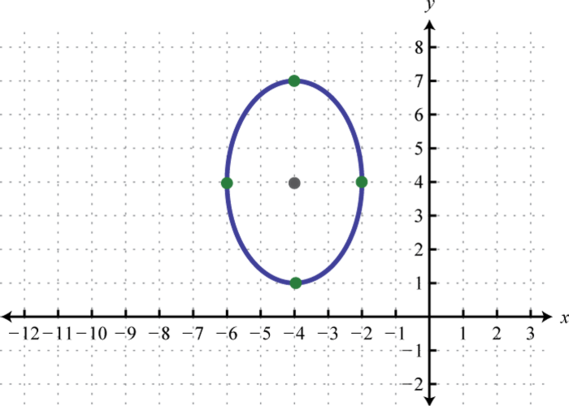What is the equation of this ellipse?

( x + 4 ) 2 4 + ( y − 4 ) 2 9 = 1 \frac {(x+4)^{2}}{4}+\frac {(y-4)^{2}}{9}=1 ( x − 4 ) 2 4 + ( y + 4 ) 2 9 = 1 \frac {(x-4)^{2}}{4}+\frac {(y+4)^{2}}{9}=1 ( x − 4 ) 2 4 + ( y + 4 ) 2 9 = 6 \frac {(x-4)^{2}}{4}+\frac {(y+4)^{2}}{9}=6 ( x + 4 ) 2 4 + ( y − 4 ) 2 9 = 36 \frac {(x+4)^{2}}{4}+\frac {(y-4)^{2}}{9}=36 ( x + 4 ) 2 4 + ( y + 4 ) 2 9 = 1 \frac {(x+4)^{2}}{4}+\frac {(y+4)^{2}}{9}=1 ( x + 4 ) 3 4 + ( y − 4 ) 3 9 = 1 \frac {(x+4)^{3}}{4}+\frac {(y-4)^{3}}{9}=1

Margaret Zheng by Margaret Zheng , 20, USA

This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try refreshing the page, (b) enabling javascript if it is disabled on your browser and, finally, (c) loading the non-javascript version of this page . We're sorry about the hassle.

1 solution

Margaret Zheng
Apr 6, 2016

Relevant wiki: Ellipse

The general equation for an ellipse in standard form is ( x − x ′ ) 2 a 2 + ( y − y ′ ) 2 b 2 = 1. \frac{(x-x')^2}{a^2} + \frac{(y-y')^2}{b^2} = 1.

The center of this ellipse is ( − 4 , 4 ) (-4,4) . Therefore, we are looking for " ( x + 4 ) (x+4) " and " ( y − 4 ) (y-4) " in our answer.

Then, notice that the horizontal axis of the ellipse (which is the minor axis for this particular case) has length 4. The vertical axis has length 6. Our a a and b b are, therefore, 2 and 3 respectively.

Plugging in those values, we get ( x + 4 ) 2 2 2 + ( y − 4 ) 2 3 2 = 1. \frac{(x+4)^2}{2^2} + \frac{(y-4)^2}{3^2} = 1. , or ( x + 4 ) 2 4 + ( y − 4 ) 2 9 = 1. \frac{(x+4)^2}{4} + \frac{(y-4)^2}{9} = 1.

4 Helpful 0 Interesting 0 Brilliant 0 Confused

I saw ( x + 4 ) 3 (x+4)^3 as ( x + 4 ) 2 (x+4)^2 ...

Pepper Mint - 3 years, 5 months ago

0 pending reports

×

Problem Loading...

Note Loading...

Set Loading...