Heron formula?
Triangle A B C has A B = 2 0 and B C : A C = 2 1 : 2 9 . What's the largest area that this triangle can have?
The answer is 304.5.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
4 solutions
Hi Chris! I think you solved the problem for the reciprocal of the given ratio. Nevertheless, due to symmetry, both, the way of thinking and the result are correct, lucky you. :)
Let B C = 2 1 k and A C = 2 9 k . Let s = 2 A B + B C + C A = 2 5 k + 1 0 . Using Heron's formula, the area of traingle A B C is s ( s − A B ) ( s − B C ) ( s − C A ) = ( 2 5 k + 1 0 ) ( 2 5 k − 1 0 ) ( 1 0 + 4 k ) ( 1 0 − 4 k ) = 1 0 0 ( k 2 − 2 5 4 ) ( 4 2 5 − k 2 )
By AM-GM inequality, ( k 2 − 2 5 4 ) ( 4 2 5 − k 2 ) ≤ 2 ( k 2 − 2 5 4 ) + ( 4 2 5 − k 2 ) = 2 0 0 6 0 9 , which the equality holds if and only if k 2 − 2 5 4 = 4 2 5 − k 2 , that is k = 3 . 2 0 5 (achievable).
So, the largest area is 1 0 0 × 2 0 0 6 0 9 = 3 0 4 . 5
Very nice problem and 'neat' solution!
I would suggest using \dfrac instead of \frac in order to make some of the fractions look larger. Anyway, it isn't a big a deal, just thought it was worth mentioning.
Log in to reply
Thanks for the suggestion. I edited it, it does look better. :)
I rather used derivative to find maximum possible area
 It is known that, on a plane, the locus of points
C
such that have a given ratio of distances from two fixed points
A
and
B
is is a circle (called a
circle of Apollonius
). If
P
is a point on segment
A
B
such that
∣
∣
P
A
∣
∣
∣
∣
P
B
∣
∣
=
r
and
Q
is its harmonic conjugate with respect to
B
and
A
(i.e.
Q
is on line
A
B
, outside segment
A
B
such that it has the same ratio of distances from
B
and
A
), then
P
Q
is a diameter of this circle.
It is known that, on a plane, the locus of points
C
such that have a given ratio of distances from two fixed points
A
and
B
is is a circle (called a
circle of Apollonius
). If
P
is a point on segment
A
B
such that
∣
∣
P
A
∣
∣
∣
∣
P
B
∣
∣
=
r
and
Q
is its harmonic conjugate with respect to
B
and
A
(i.e.
Q
is on line
A
B
, outside segment
A
B
such that it has the same ratio of distances from
B
and
A
), then
P
Q
is a diameter of this circle.
In our case, this ratio is
r
=
2
9
2
1
. For simplicity, we ‘ll use the label of any segment to denote both the segment and its length. For instance,
A
B
=
2
0
. Let’s calculate the length of this diameter using properties of proportions.
Referring to the figure, P A P B = 2 9 2 1 ⇒ P A + P B P B = 2 9 + 2 1 2 1 ⇒ A B P B = 5 0 2 1 ⇒ P B = 5 0 2 1 × 2 0 ⇒ P B = 5 4 2 Q A Q B = 2 9 2 1 ⇒ Q A − Q B Q B = 2 9 − 2 1 2 1 ⇒ A B Q B = 8 2 1 ⇒ Q B = 8 2 1 × 2 0 ⇒ Q B = 2 1 0 5 Hence, P Q = P B + B Q = 5 4 2 + 2 1 0 5 = 1 0 6 0 9 Since side A B of △ A B C has a fixed length, its area gets maximised, when the corresponding altitude is the longest possible h max . Obviously, this altitude is the radius of the Apollonian circle mentioned above, i.e. h max = 2 P Q = 2 0 6 0 9 . Concluding, the largest area that △ A B C can have is [ A B C ] max = 2 1 A B ⋅ h max = 2 1 × 2 0 × 2 0 6 0 9 = 3 0 4 . 5
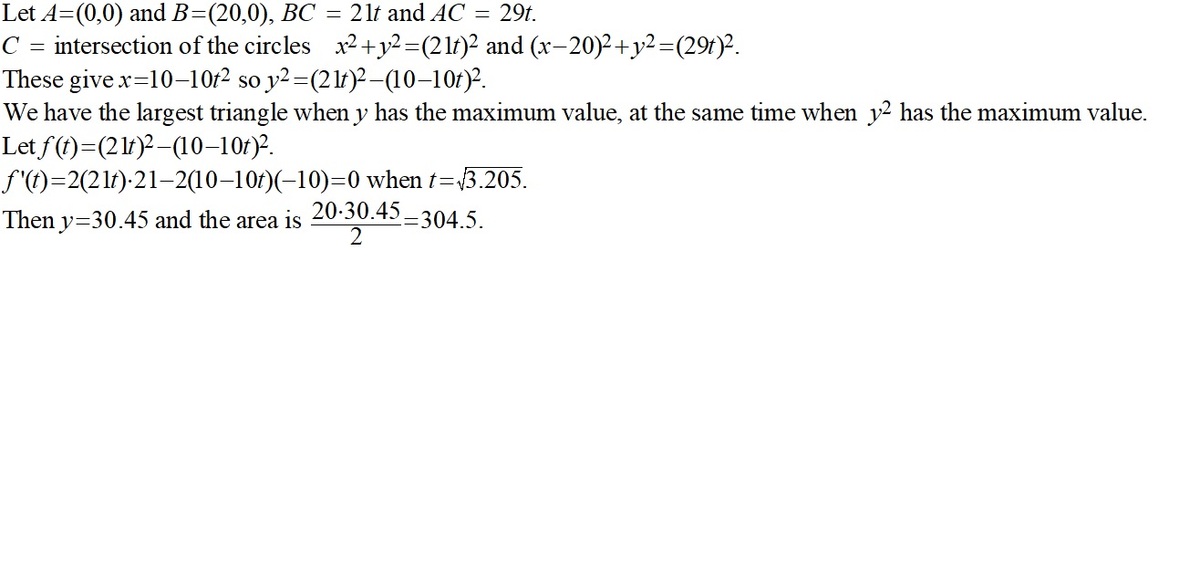
I did this exactly the same way as @Chan Lye Lee , but for an alternative approach: let the coordinates of A be ( − 1 0 , 0 ) and B ( 1 0 , 0 ) . Then point C ( x , y ) satisfies 2 1 2 ( x + 1 0 ) 2 + y 2 = 2 9 2 ( x − 1 0 ) 2 + y 2
This is a circle with centre ( 2 0 − 6 4 1 , 0 ) and radius 2 0 6 0 9 :
The base of Δ A B C is fixed ( A B = 2 0 ; its height is the y -coordinate of C , which is greatest when C is directly above the centre of the circle; so the largest possible area is 2 1 × 2 0 × 2 0 6 0 9 = 2 6 0 9