Heron kills it
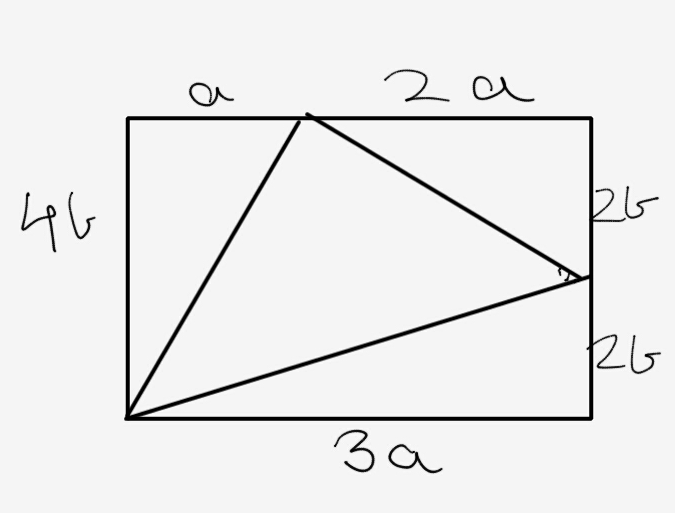
A triangle with sides of a 2 + 1 6 b 2 , 9 a 2 + 4 b 2 , and 2 a 2 + b 2 such that a and b are positive integers with area 3 0 is given. Find the number of ordered pairs ( a , b ) that satisfy this restriction.
The answer is 4.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
Using Heron's formulae for triangle area with sides x , y , z where the area is 4 1 2 x 2 y 2 + 2 y 2 z 2 + 2 z 2 x 2 − x 4 − y 4 − z 4 , we subsitute x = a 2 + 1 6 b 2 , y = 9 a 2 + 4 b 2 , z = 4 a 2 + 4 b 2 , expand and then reduce our expression to get an area of:
4 1 2 ( ( a 2 + 1 6 b 2 ) ( 9 a 2 + 4 b 2 ) + ( 9 a 2 + 4 b 2 ) ( 4 a 2 + 4 b 2 ) + ( 4 a 2 + 4 b 2 ) ( a 2 + 1 6 b 2 ) ) − ( ( a 2 + 1 6 b 2 ) 2 + ( 9 a 2 + 4 b 2 ) 2 + ( 4 a 2 + 4 b 2 ) 2 )
= 4 1 4 0 0 a 2 b 2 = 5 a b = 3 0
We thus desire to find all ordered pairs of positive integers ( a , b ) where a b = 6 . There are then 4 such pairs: ( 1 , 6 ) , ( 2 , 3 ) , ( 3 , 2 ) , ( 6 , 1 ) .
 proof without words
proof without words