Hexa-Integer

Geometry Level 3

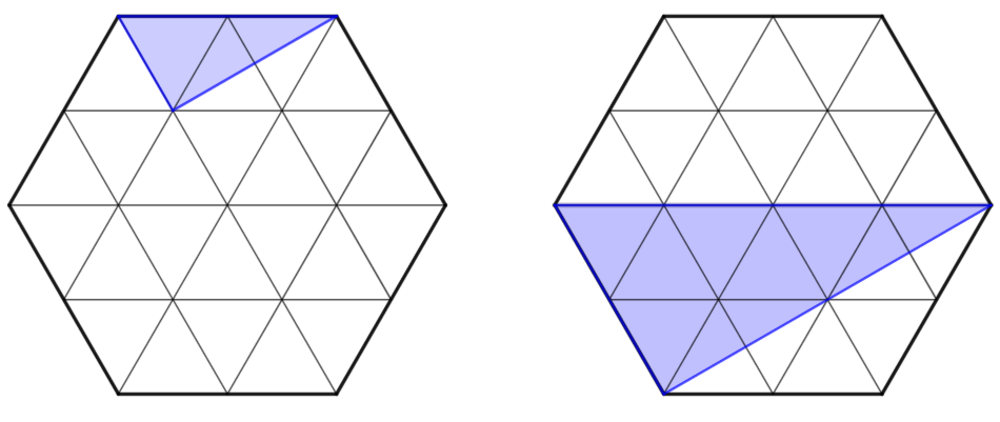$Both diagrams show that for hypotenuse lengths $2$ and $4$ the right triangle can be constructed by taking two vertex points on the edges of the hexagon. But must that be the only case for regular hexagon of $24$ unit equilateral triangles?$ Both diagrams show that for hypotenuse lengths $2$ and $4$ the right triangle can be constructed by taking two vertex points on the edges of the hexagon. But must that be the only case for regular hexagon of $24$ unit equilateral triangles?

The regular hexagon of side length $2$ consists of $24$ unit equilateral triangles. As shown above, we can select two distinct points on its perimeter (not necessarily the vertex points of two unit equilateral triangle), such that:

The distance between these points is an integer.
It is the hypotenuse of the right triangle.
In addition, the triangle passes through one vertex point, which forms the right angle.

Does there exist a right triangle whose hypotenuse length is $3$ ?

Inspiration. (See solutions.)

Yes No

1 solution

Thanos Petropoulos
Feb 19, 2021

Let $ABCDEF$ be the regular hexagon. Consider the vertex point $P$ , which is the intersection of lines $FC$ and $AE$ . A right angle starts pivoting around $P$ from position $\angle FPA$ , until it reaches position $\angle APC$ (as seen in the animation). At any time, the sides of the right angle intersect the sides of the hexagon at points $Q$ and $R$ . During this movement, the length of the hypotenuse $QR$ of $\triangle PQR$ changes continuously . In the beginning, $QR=FA=2$ and in the end $QR=AC=2\sqrt{3}$ .

Since $2<3<2\sqrt{3}$ , by Intermediate Value Theorem , there exists a moment when $QR=3$ . The answer is $\boxed{Yes}$ .

Sir this is beyond brilliant

Utkarsh Kumar - 3 months, 2 weeks ago

Thank you! I'm glad you liked it.

Thanos Petropoulos - 3 months, 2 weeks ago

Hexa-Integer

1 solution

0 pending reports