Hexagonal Circuit

See the whole circuits as combination of $1 \Omega \times 2~and~\frac12 \Omega \times 5,$

1st step: $(1 \Omega + \frac12 \Omega) // \frac12 \Omega = 0.375 \Omega$

2nd step: $(0.375 \Omega + 0.5 \Omega) // 0.5 \Omega = \frac{7}{22} \Omega$

3rd step: $(\frac{7}{22} \Omega + \frac12 \Omega) // 1 \Omega = \frac{9}{20} \Omega$

Here's a "virtual experiment" approach. Apply a 1-volt source, as shown.

Write nodal equations (condensed versions shown):

$3 V_1 - V_2 = 1 \\ -V_1 + 3 V_2 - V_3 = 0 \\ -2 V_2 + 3 V_3 = 0$

Solve for the three voltages (using a computer). Then calculate the current out of the voltage source:

$I = 1 + 2 (1 - V_1)$

Then the overall resistance is:

$R_T = \frac{1}{I}$

The answer comes out to 0.45

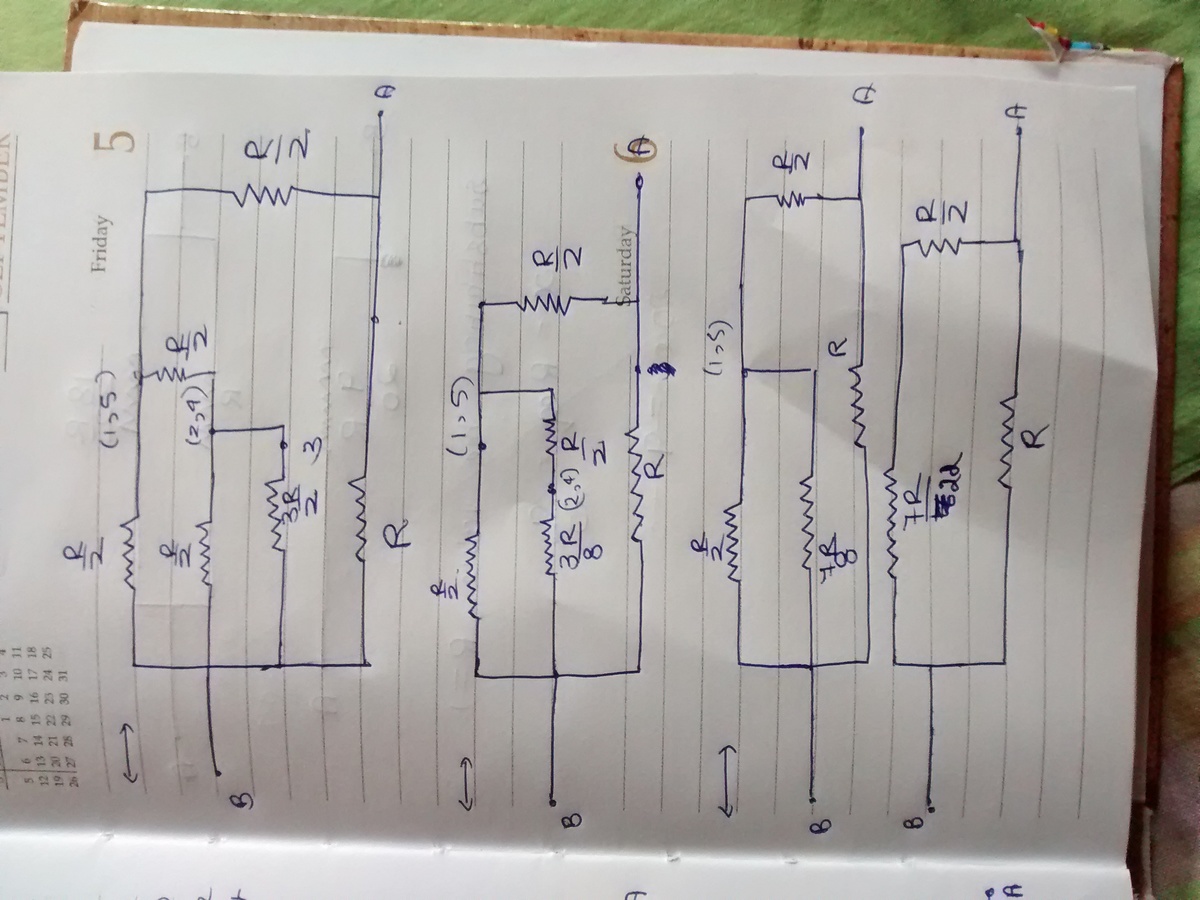
$The~ \color{#20A900}{Green},~\color{#D61F06}{ Red}, ~and~ \color{#3D99F6}{ Blue} ~\text{Star connections are converted in to Delta. Fig.1 to Fig 2.}\\ \text{BA, BC, and BD each will have now three resistances in parallel, 3, 1 and 3}\\ \text{ reduces to single 3/5. Fig 3}\\ \text{Star at D is converted to Delta, as the}~ \color{#20A900}{Green}~\text{ lines in Fig. 3 to Fig. 4. D vanishes.}\\ \text{This creates three pairs of two parallel resistances between A, B, and C. }\\ \text{Each pair is replaced by a single resistance as shown in Fig.5}\\ \text{AC and CB are in series, and added as shown in Fig. 6.}\\ \text{The last parallel pair in AB is replaced by a single resistance 9/20=0.45 }$

Great solutions everyone! Here an alternative approach, more elementary, and outside the box:

Suppose the circuit is connected to a voltage $V$ such that the current through the wire opposite $AB$ is 1 A. Using symmetry and Kirchhoff's current law, we immediately determine the two adjacent currents to be 1/2 A.

To find the current marked '?', consider that the voltages and currents in each wire should have the same numerical value. Applying Kirchhoff's voltage law, we find that the voltage should be 1 + 1/2 = 3/2 V, and therefore the current is 3/2 A.

Using the current law again:

Once again the voltage law helps to find the next voltage and current: 2 + 3/2 = 7/2. Continuing along the same lines we find:

Since the wire $AB$ has 9 A of current and a resistance of 1 ohm, the applied voltage must have been 9 V.

The total current flowing out of point A is 11/2 + 11/2 + 9 = 20 A. (It is easy to check that the current flowing into B is also 20 A, as it should be.)

Conclusion: $R = \frac V I = \frac{9\ \text{V}}{20\ \text{A}} = \boxed{0.45\ \Omega}.$