Hexagon-ally Closer

Calculus Level 5

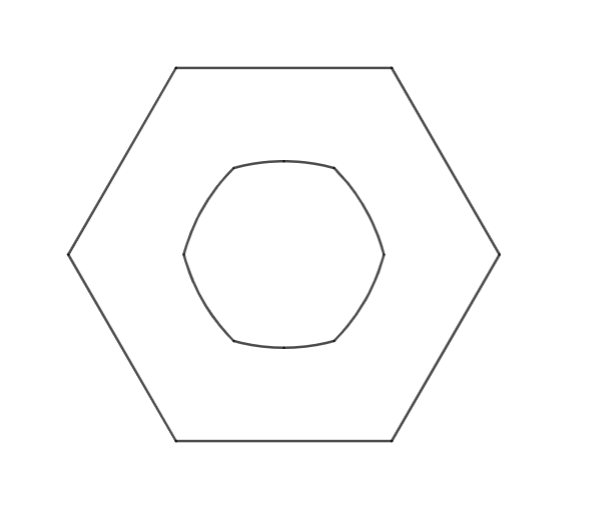
The figure shows a regular hexagon whose in-radius is 1 1 ,the figure inside is the boundary of region which is made up of all points that are closer to the center of the hexagon than any of it's side.

Find the area of the region inside.


The answer is 0.8230.

Shauryam Akhoury by Shauryam Akhoury , 18, India

This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try refreshing the page, (b) enabling javascript if it is disabled on your browser and, finally, (c) loading the non-javascript version of this page . We're sorry about the hassle.

2 solutions

Taking centre of the hexagon as the origin, the top curve is given by y=(1/2)(1-x^2) which intersects the radius y=x√3 at (2-√3, 2√3-3). The area asked is 12 times the integral of [(1/2)(1-x^2)-x√3] dx from 0 to 2-√3, which is equal to 2(16-9√3) = 0.82308546376

3 Helpful 1 Interesting 1 Brilliant 1 Confused

Consider the upper edge of the hexagon and write its equation (y=1) then write an equation of a curve which equally distant from origin as well as this line: sqrt(x^2+y^2)=|y-1| squaring and exchanging gives an equation y=1/2(1-x^2) but this is the equation of the curve ranging from mid points of the upper diagonals i.e. (-1/2√3,1/2) to (1/2√3,1/2) Integrating the curve in this range and subtracting areas of the 2 triangles formed by origin, one of the above point with x axis will give the area of a small section. Then multiply this value with 6 will give the required area.

1 Helpful 0 Interesting 0 Brilliant 0 Confused

0 pending reports

×

Problem Loading...

Note Loading...

Set Loading...