Hexagon in a Hexagon

We work this out by working out the area of the hexagon and taking away the area of the triangles GBH, HCI and so on.

Let the length of the side of the hexagon be $a$ .

Then the area of the hexagon $\frac{\sqrt{3}}{4} a^2 \times 6 = \frac{3\sqrt{3}}{2} a^2$

Let the (random) length of AG is x, and the (random) length of BH be y. Then the length GB is (a-x).

The expectation of the area of the triangle GBH is the expectation of $\frac{1}{2} (a-x)(y) sin(120 ^ \circ)$ .

Expanding we get $\frac{\sqrt{3}}{4} (ay-xy)$

Using linearity of expectation we have E(area GBH)= $\frac{\sqrt{3}}{4} \times (aE(y)-E(xy))$

Using the fact that x and y are independent, we have E(xy)=E(x)*E(y)

We have E(x)=E(y)=a/2

So putting the results together, we have E([GBH])= $\frac{\sqrt{3}}{16} a^2$

Using linearity of expectation once again the Expectation of all 6 areas= $\frac{3\sqrt{3}}{8} a^2$

So the expected area = $\frac{3\sqrt{3}}{2} a^2 - \frac{3\sqrt{3}}{8} a^2$ = $\frac{9\sqrt{3}}{8} a^2$

Substituting the numbers gives 54

Let $s = 4 \cdot 3^{1/4}$ be the side length of the hexagon. Note $|ABCDEF| = 6(s/2)(s\sqrt{3}/2) = 6 \cdot (2 \cdot 3^{1/4})^2 \sqrt{3} = 72$ . Suppose without loss of generality that $G$ lies on $FA$ , $H$ lies on $AB$ , $I$ lies on $BC$ , etc. Then the random area $|GHIJKL|$ equals $|ABCDEF| - (|GAH|+|HBI|+\cdots+|LFG|)$ , and by the linearity of expected value, ${\rm E}[|GHIJKL|] = 72 - ({\rm E}[|GAH|] + {\rm E}[|HBI|] + \cdots + {\rm E}[|LFG|]) .$ Now consider a single triangle. Since $\angle GAH = 120^\circ$ , we have $|GAH| = \frac{1}{2}(GA)(AH) \sin 120^\circ = \frac{\sqrt{3}}{4}(GA)(AH).$ But because $G$ and $H$ are chosen uniformly at random and independently of each other, the expected value of the product of the random lengths $GA$ and $AH$ is equal to the product of their individual expected values; i.e., ${\rm E}[(GA)(AH)] = {\rm E}[GA]{\rm E}[AH] = (s/2)^2,$ as the mean lengths of the segments $GA$ and $AH$ are half the lengths of $FA$ and $AB$ , respectively. Hence ${\rm E}[|GAH|] = \frac{\sqrt{3}}{4}(s/2)^2 = 3.$ And because the expected value for each of the other 5 triangles is computed similarly, the sum of their expected values is simply $6 \cdot 3 = 18$ , from which it follows that the expected value of $|GHIJKL|$ is $72 - 18 = 54$ .

Note that E(GHIJKL) = (ABCDEF) - E(GAH) - E(HBI) - ... - E(LFG).

The area ABCDEF can be determined easily using a hexagon area formula to be 72. Further, notice that all of the small triangles have expected area equal to $\frac{1}{2} E(GA)E(AH) \sin(120)$ , since GA and AH are independent.

But $E(GA) = E(AH) = 2 \sqrt[4]{3}$ , giving an expected area of 3.

Thus, the overall expected area is 72 - 18 = 54.

E(S(small triangle))=E(1/2 x y sqrt(3)/2)=sqrt(3)/4 E(x) E(y)=sqrt(3)/16 a^2 E(S(ABCDEF))=sqrt(3)/4 6 a^2 a=4(3)^(1/4)

If I have stick of length L and I am choosing point randomly on that stick than , expected value can be counted like below : Think that one end of stick is at origin and stick 's length is towards positive x-axis . We can think that stick is made of n small pieces . So, E(x) = (1/n) 0+(1/n) (L/n)+(1/n) (2L/n)+....... + (1/n) ((n-1)L/n) = (L/n^2) (n (n-1))/2

As , n-> infinity , E(x) = L/2 .

So , G,H,I,J,K,L are midpoints of original Hexagon . Square of Side of this Hexagon let's say GH^2 = ( 2∜3 )^2 + (2 ∜3 )^2 - 2 (2∜3) (2∜3) cos(120) = 12√ 3 . As, area of regular Hexagon = 3√ 3/2 * (GH)^2 = 54 .

Solution 1:

Let $O$ be the center of the hexagon. We draw the below figure.

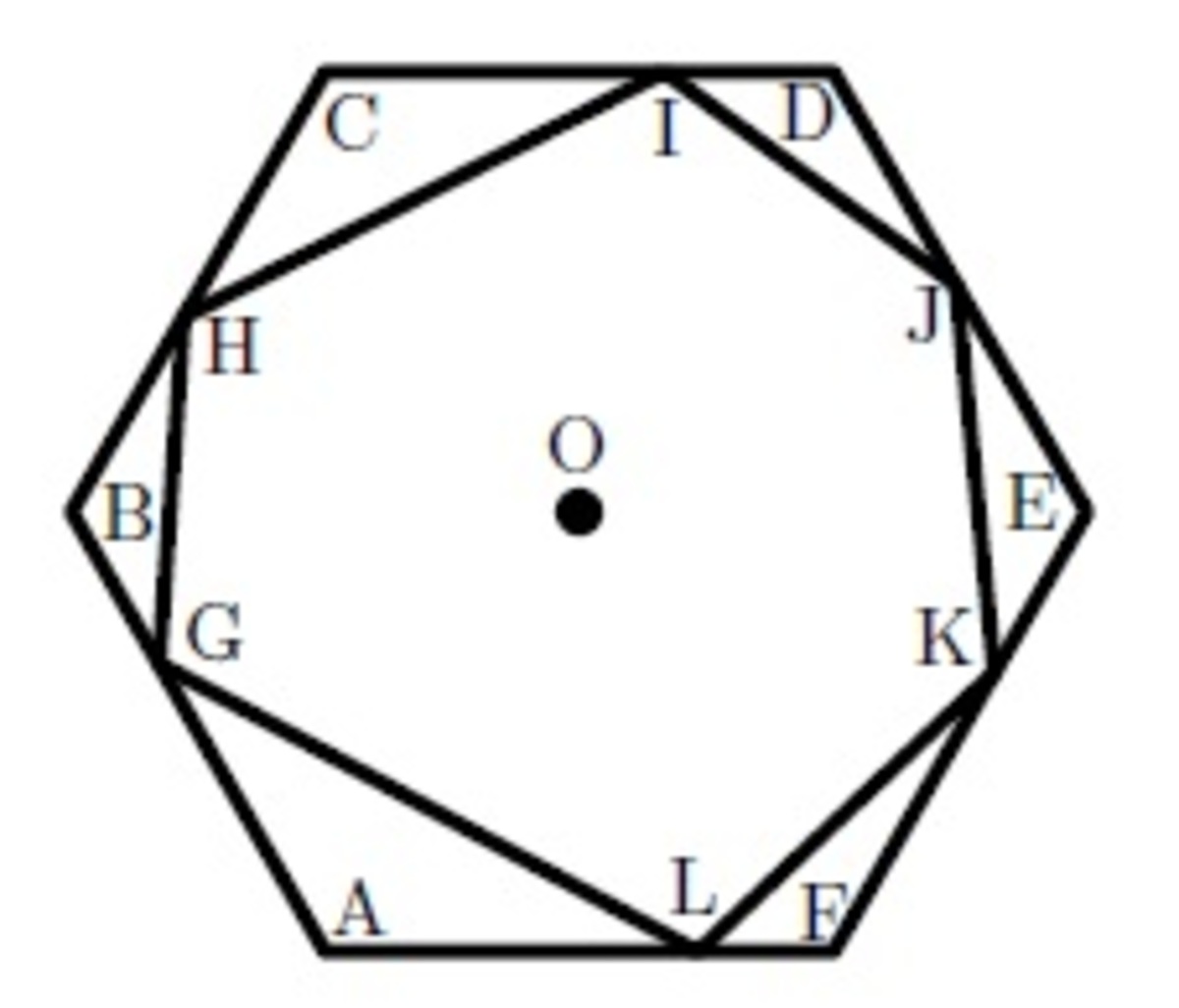
We observe that $E([GHIJKL])$ is equal $[ABCDEF]$ minus the expected areas of the small triangles.

We calculate $E([LAG]).$ The area of triangle $LAG$ is equal to $\frac{AL \times h}{2}$ where $h$ is the perpendicular distance from $AL$ to $G,$ so the expected area is $E\left(\frac{AL \times h}{2}\right).$ However, we observe that $h$ and $AL$ are independent, since the choice of positions of $L$ and $G$ are independent. So the expected area is $\frac{E(AL)E(h)}{2}.$ By symmetry, it is clear to see that $E(AL) = \frac{AF}{2}$ and the expected value of $h$ is half of the perpendicular distance from $AF$ to $B.$ Since this is a regular hexagon, this is the same as half the perpendicular distance from $AF$ to $O.$ Thus, we have that $E([LAG]) = \frac{[AFO]}{4} = \frac{[ABCDEF]}{24}.$ We see that this is also the case for the other 5 triangles. Thus, $E([GHIJKL]) = [ABCDEF] - \frac{[ABCDEF]}{4} = \frac{3[ABCDEF]}{4}$

The area of a regular hexagon is $\frac{3\sqrt{3}}{2}s^2$ where $s$ is the length of a side. Thus, the area of $ABCDEF$ is $\frac{3\sqrt{3}}{2}(4\sqrt[4]{3})^2 = 72$ and the expected area of $GHIJKL$ is $\frac{3 \times 72}{4} = 54.$

Solution 2:

Let $G^*, H^*, I^*, J^*, K^*, L^*$ denote the midpoints of the corresponding sides. By considering triangle $HGL$ , you can show that $E[GHIJKL] = E[G^*HIJKL]$ . Proceed along by considering triangles $G^*HI, H^*IJ, \ldots$ , we get that

$E[GHIJKL] = E[G^*HIJKL] = E[G^*H^*IJKL] = E[G^*H^*I^*JKL] = E[G^*H^*I^*J^*K^*L] = E[G^*H^*I^*J^*K^*L^*].$

For simplicity, the points G , H , I , J , K , L are chosen to be the mid points of the sides AB , BC , CD , DE , EF and FA respectively. Thus GHIJKL is a regular hexagon. Let O be the point of intersection of all diagonals of ABCDEF and GHIJKL .

Thus in triangle OAB , OA = OB = 4\sqrt[4]{3}

Also in triangle OAG , OG = OA \sin 60^\circ = 2 3^{\frac {3}{4} }

And in triangle OGH , OG = GH = 2 3^{\frac {3}{4} }

Thus area of hexagon GHIJKL = \frac { 3 \sqrt{3} } {2} } {2 3^{\frac {3}{4} } }^2 = 54

because G,H,I,J,K,L are chosen uniformly at random one from each side of the hexagon and also form hexagon,

to simplify our mathematics problem just, make that point in the middle of Side, like G is the middle of side AB, etc

then you find the smaller hexagon GHIJKL inside the Hexagon ABCDEF

Make an Point named O in the middle of 2 Hexagon

And In Equilateral Triangle AOB which AB=4*3^(1/4)

there are Line OG which is 2 3^(3/4) (collected from special phytagoras a,a sqrt(3),2a)

then let we could the area of Equilateral GOH using 1/2 GO OH*sin Teta, Teta = 60 Degree because of its Equilateral Triangle

you can find the Area Of hexagon GHIJKL by sum of total GOH, HOI, IOJ, JOK, KOL, LOG

1/2* (2 3^(3/4)) * (2 3^(3/4)) * sqrt(3)/2 * 6 = 54

If we think it logically, no matter what you put uniformly at random those points G, H, I, J, K and L in each sides of the hexagon ABCDEF, the area of the hexagon GHIJKL is still same with the area of its hexagon in the form of equilateral triangle. So, we can assumption that hexagon GHIJKL is equilateral hexagon to make the calcuklation easier. Suppose point H, I, J, K ,L & G consecutively in AB, BC, CD, ED, EF, & AF. Then, take a look at triangle AHG, which are $\angle GAH = 120 ^ \circ$ & $\angle AGH=\angle AHG = 30 ^ \circ$ . Since AB = BC = CD = DE = EF = FA = $4\sqrt[4]{}$ , and triangle AHG is isosceles with AG = AH = $2\sqrt[4]{3}$ , with the law of sinus we get GH $2\sqrt[4]{27}$ . Back to my beginning assumption, that GHIJKL is eqiulateral hexagon, with sides length $2\sqrt[4]{3}$ .

Since an equilateral hexagon consist of six equilateral triangle with both of them have an equal area. We can conclude that each small triangle have an area $\frac{1}{4}s^{2}\sqrt{3}$ which the value of s is the length of the sides of the hexagon GHIJKL, $2\sqrt[4]{3}$ . Suppose O is the center of the hexagon, so ;

[GHO]= \frac{1}{4}{\(2\sqrt[4]{3}}^{2}\sqrt{3} [GHO]= $\sqrt[4]{81}$ [GHO]=9

Since

[GHIJKL]=6 x [GHO] [GHIJKL]=6x9 [GHIJKL]=54

CMIIW