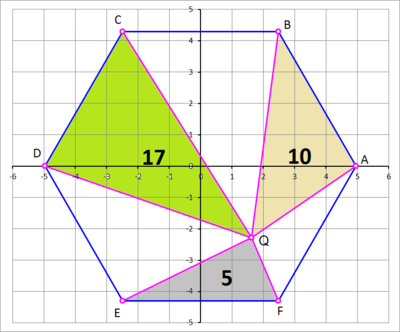
Hexagon Interior Point
A regular hexagon A B C D E F is centered at the origin and has vertex A lying on the positive x -axis, and the labelling is counter clockwise. A point Q = ( Q x , Q y ) lies inside the hexagon, such that [ Q A B ] = 1 0 , [ Q C D ] = 1 7 , and [ Q E F ] = 5 . If R is the circumradius of the hexagon (which is also equal to the side length), then find ⌊ 1 0 0 0 ( R + Q x + Q y ) ⌋ .
The answer is 4308.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
Frankly, I suspect, the two sums of areas of alternate internal triangles of a regular polygon of even number of sides are equal. The proof for hexagon is given below. Therefore 1 0 + 1 7 + 5 = 3 2 is half the area of the regular hexagon. Then the area of the regular hexagon is 6 4 and the area of one of the six central equilateral triangle is 6 6 4 and 4 3 R 2 = 6 6 4 ⟹ R = 3 8 2 3 ≈ 4 . 9 6 3 2 2 5 9 1 5 .
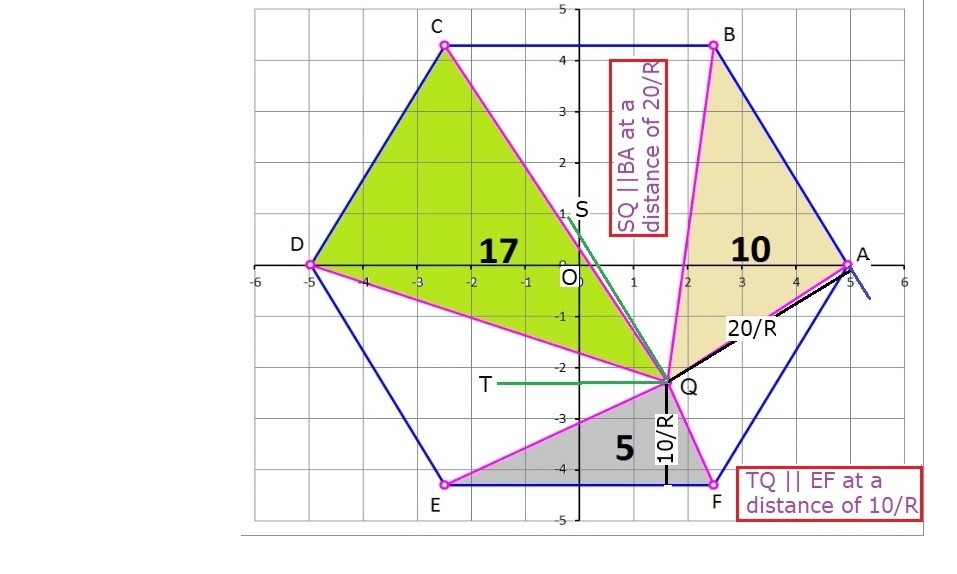
Consider △ Q E F , let its height be h , then [ Q E F ] = 2 1 h E F = 5 . Since E F = R , ⟹ h = R 1 0 . Therefore, Q y = − 2 3 R + h = − 2 3 R + R 1 0 ≈ − 2 . 2 8 3 4 6 1 1 0 5 .
Consider △ Q A B , we can find its area using the coordinates of its vertices as follows:
2 ( Q x − A x ) ( Q y + A y ) + 2 ( A x − B x ) ( A y + B y ) + 2 ( B x − Q x ) ( B y + Q y ) ( O x − R ) ( O y + 0 ) + ( R − 2 R ) ( 0 + 2 3 R ) + ( 2 R − Q x ) ( 2 3 R + Q y ) 2 3 R 2 − 2 3 R Q x − 2 1 R Q y R − Q x − 3 Q y ⟹ Q x = [ Q A B ] = 1 0 = 2 0 = 2 0 = 3 R 4 0 = 2 3 R − 3 R 5 0 ≈ 1 . 6 2 8 5 5 8 5 0 3
Therefore, ⌊ 1 0 0 0 ( R + Q x + Q y ) ⌋ = 4 3 0 8 .
Proof: Using coordinates of vertices to find the area of triangle:
⎩ ⎪ ⎨ ⎪ ⎧ [ Q A B ] = 4 3 R 2 − 4 1 R Q y − 4 3 R Q x [ Q C D ] = 4 3 R 2 − 4 1 R Q y + 4 3 R Q x [ Q E F ] = 4 3 R 2 + 2 1 R Q y
⟹ [ Q A B ] + [ Q C D ] + [ Q E F ] = 4 3 3 R 2 = 2 1 [ A B C D E F ] .
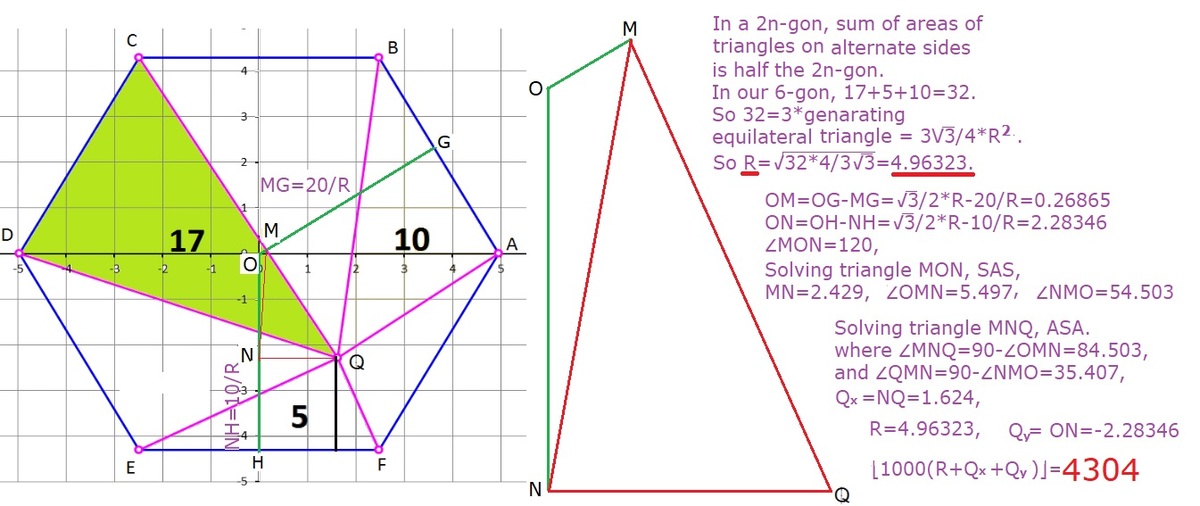
Extend sides A B , C D , and E F to make equilateral △ M N P , as shown below:
△ M N P is made up of 9 equilateral triangles, 6 of which make up hexagon A B C D E F . Therefore, A △ M N P = 2 3 A A B C D E F .
△ M N P is also made up of triangles △ M Q N , △ M Q P , and △ N Q P , so A △ M N P = A △ M Q N + A △ M Q P + A △ N Q P .
△ A Q B has the same height but a base that is 3 1 that of △ N Q P , so A △ A Q B = 3 1 A △ N Q P . Likewise, A △ C Q D = 3 1 A △ M Q P and A △ E Q F = 3 1 A △ M Q N .
Therefore, A △ A Q B + A △ C Q D + A △ E Q F = 3 1 ( A △ N Q P + A △ M Q P + A △ M Q N ) = 3 1 ( A △ M N P ) = 3 1 ( 2 3 A A B C D E F ) = 2 1 A A B C D E F .
In the problem, A △ A Q B = 1 0 , A △ C Q D = 1 7 , A △ E Q F = 5 , and A A B C D E F = 2 3 3 R 2 , so 1 0 + 1 7 + 5 = 2 1 ⋅ 2 3 3 R 2 which solves to R = 3 8 4 1 2 .
△ E Q F has an area of A △ E Q F = 5 , a base of b △ E Q F = R , and a height of h △ E Q F = Q y + 2 3 R , and using A = 2 1 b h and R = 3 8 4 1 2 this solves to Q y = − 2 4 1 7 4 1 0 8 .
△ A Q B has an area of A △ A Q B = 1 0 , a base of b △ A Q B = R , and using A = 2 1 b h it has a height of h △ A Q B = R 2 0 . As a side of an equilateral triangle with a length of 3 R on centered at the origin, N P has a slope of m = tan 1 2 0 ° = − 3 and a y -intercept of 3 2 ⋅ 2 3 3 R = 3 R , for an equation of y = − 3 x + 3 R . A line parallel to it with Q on it will have the same slope as N P but be R 2 0 away on its perpendicular, which is R 4 0 less than the N P 's y -intercept of 3 R . Therefore, Q is on the line y = − 3 x + 3 R − R 4 0 . Since Q y = − 2 4 1 7 4 1 0 8 and R = 3 8 4 1 2 , Q x solves to Q x = 8 7 4 1 2 .
Therefore, ⌊ 1 0 0 0 ( R + Q x + Q y ) ⌋ = ⌊ 1 0 0 0 ( 3 8 4 1 2 + 8 7 4 1 2 + − 2 4 1 7 4 1 0 8 ) ⌋ = 4 3 0 8 .