Hexagon 's Segment
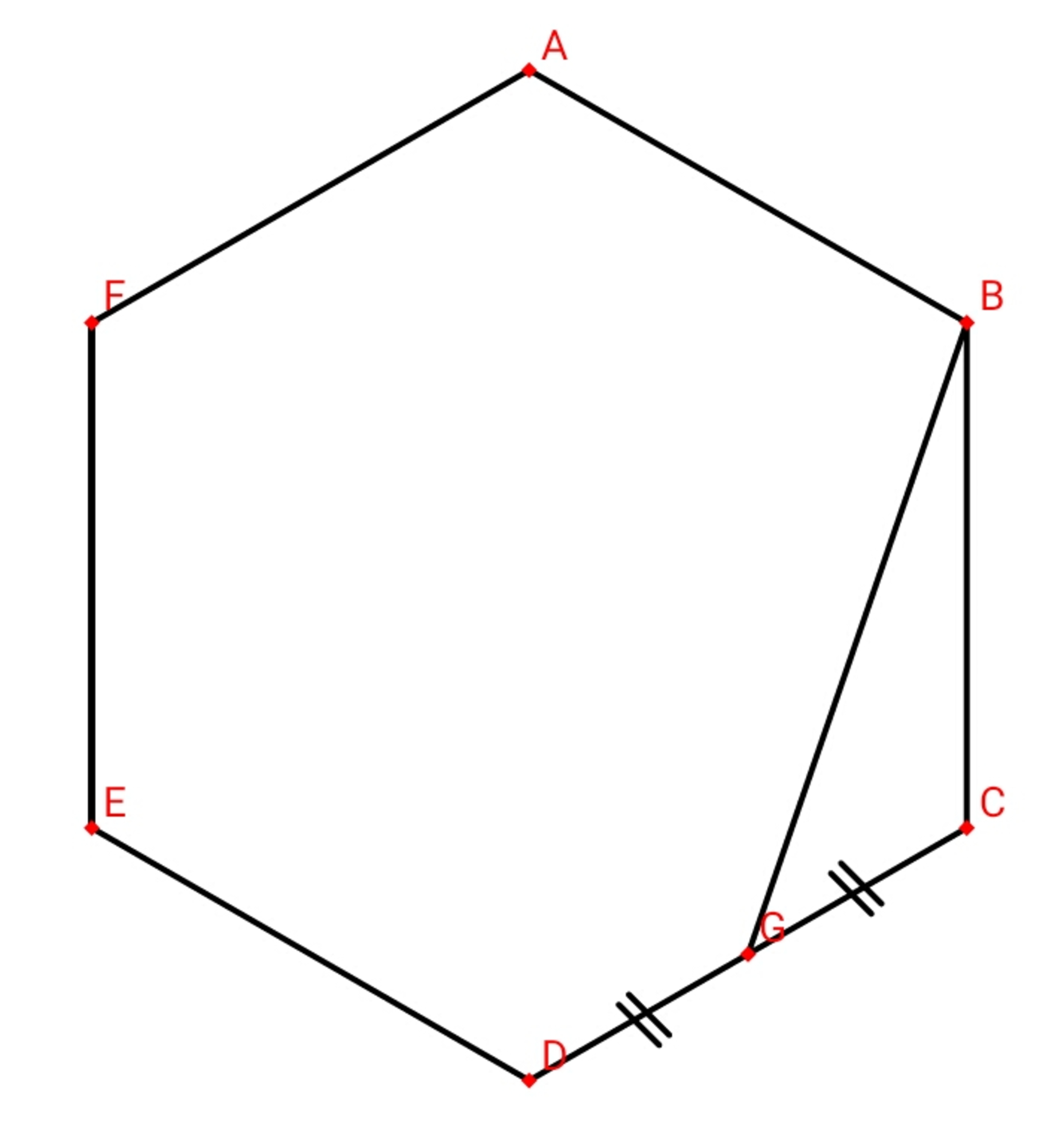
A B C D E F is a regular hexagon, with A B = 1 cm . Point G lies on D C , such that D G = G C . If the length of B G is in the form of b a cm , where a , b are coprime positive integer, with a isn't a perfect square, find a + b .
Try another problem on my set! Let's Practice
The answer is 9.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
5 solutions
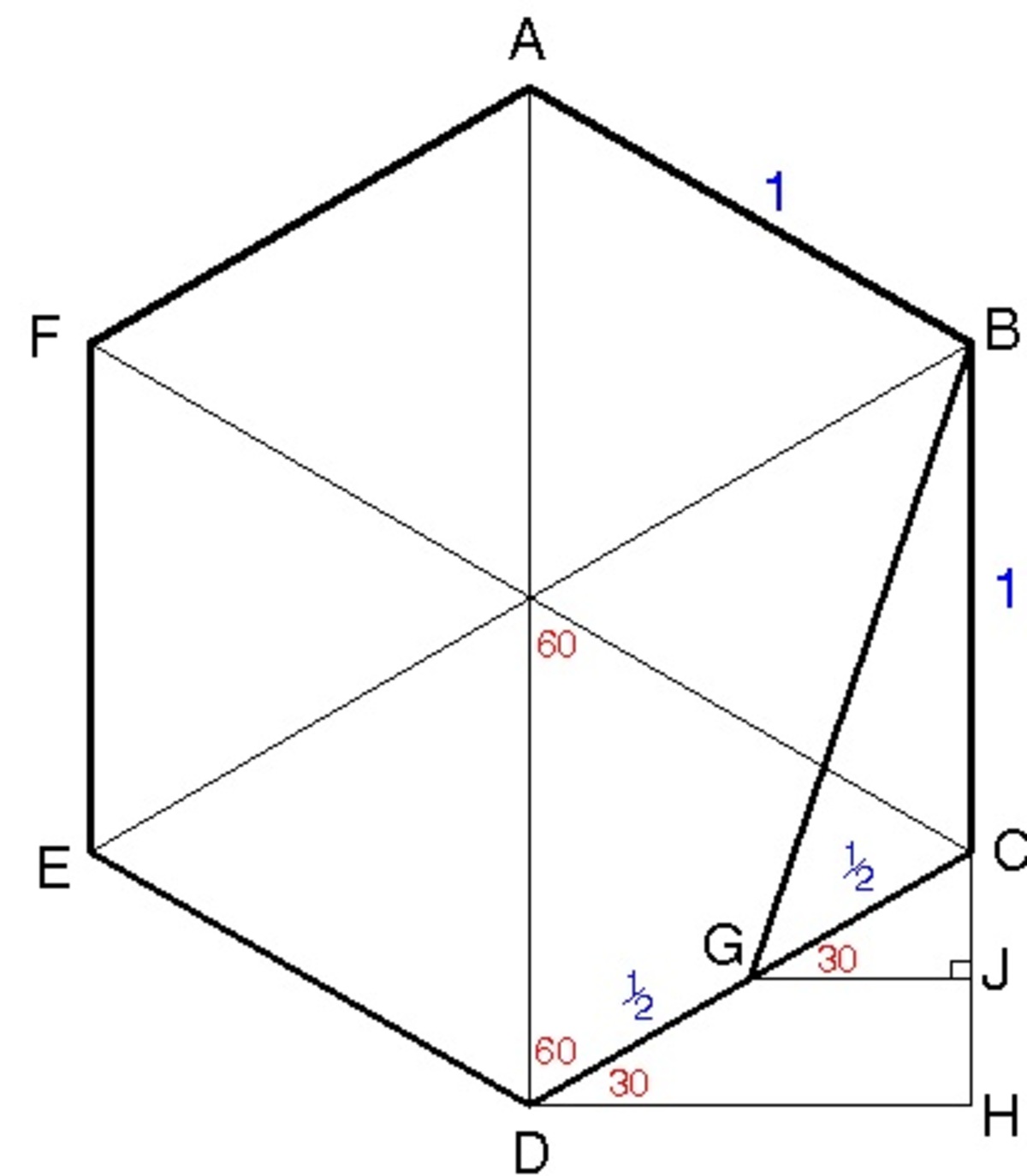
Consider △ C J G :
s i n 3 0 = 2 1 C J
2 1 = 2 1 C J
C J = 2 1 ( 2 1 ) = 4 1
G J = ( 2 1 ) 2 − ( 4 1 ) 2 = 1 6 3 = 4 3
It follows that
B J = 1 + C J = 1 + 4 1 = 4 5
Consider △ B J G , by pythagorean theorem
B G = ( 4 5 ) 2 + ( 4 3 ) 2 = 1 6 2 8 = 4 7 = 2 7
Finally,
a = 7 and b = 2
a + b = 7 + 2 = 9
Here is a solution without cosine law
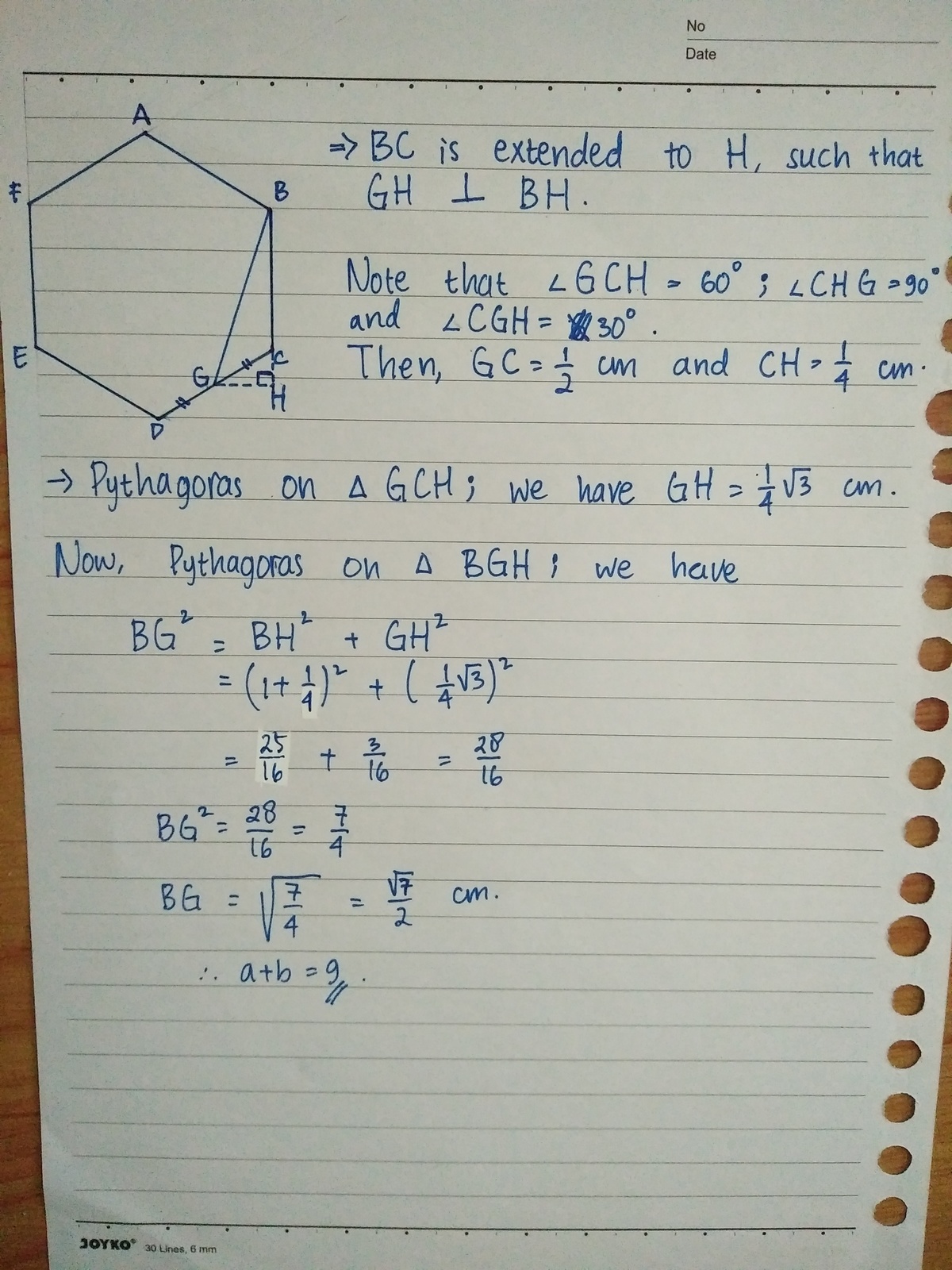
By cosine law:
B G 2 = B C 2 + C G 2 − 2 ⋅ B C ⋅ C G ⋅ cos ( ∠ B C G )
B G 2 = 1 2 + 2 1 2 − 2 ⋅ 1 ⋅ 2 1 ⋅ ( − 2 1 )
B G 2 = 4 7
B G = 2 7
So:
a = 7 , b = 2 , a + b = 9
From law of cosines in △ B C G we can get B G = 4 1 + 1 − cos 1 2 0 ∘ = 2 7
7 + 2 = 9
I too first did it this way. However seeing this solution used another method of solution.
I s o s c e l e s Δ B C D , v e r t e x ∠ 1 2 0 , ∴ b a s e , B D = 3 . T h e m e d i a n B H o f Δ B C D = 2 1 ∗ 2 ( B D 2 + B C 2 ) − D C 2 = 2 1 ∗ 2 ( 3 + 1 ) − 1 = 2 7 = b a . a + b = 9 .