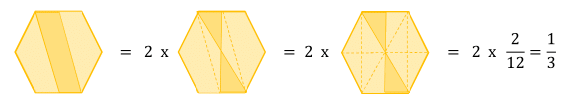Hexagon Strip
The diagonal lines join a vertex to the midpoint of the edge.
What fraction of the regular hexagon is shaded?
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
10 solutions
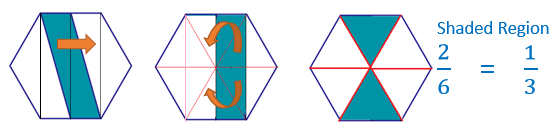
In your middle diagram, are 1 green and 1 white equal rectangles (top to bottom). The 4 white triangles (left and right) can also form 1 white equal rectangle. Thus, the green area is 1/3 of total area. - David Zak
Log in to reply
Yes. From the second diagram only we can go for the solution there are 12 equal triangles and 4 are shaded. Therefore the shaded region is 4/12=1/3. But for the nice and clear visualization I go for the third diagram.
Wonderfull and elegant solution
This problem is very interesting because visually (at least to me), the remaining white areas look bigger than the shaded area.
Log in to reply
It is a trick played by the mind. Given two objects with equal area, the object more similar to a circle looks bigger.
In the second hexagon, the darker triangle looks bigger (to me), even though the four triangles formed by the diagonals of the parallelogram all have equal area.
 A regular hexagon is composed of
6
equilateral triangles. The area of one equilateral triangle of side
s
is
4
s
2
3
. We assume that the length of one side of hexagon is
2
. Then the area of the hexagon is
A regular hexagon is composed of
6
equilateral triangles. The area of one equilateral triangle of side
s
is
4
s
2
3
. We assume that the length of one side of hexagon is
2
. Then the area of the hexagon is
A h e x = ( 6 ) 4 2 2 3 = 6 3
Now, by cosine law
x 2 = 2 2 + 2 2 − 2 ( 2 ) ( 2 ) cos 6 0 ⟹ x = 2 3
The area of the shaded region is
A s = 1 ( 2 3 ) = 2 3
Finally,
A h e x A s = 6 3 2 3 = 3 1
Steve, there are other solutions that use geometric symmetries. This is an algebraic solution. You're writing a completely new solution - not really a response to this one.
Nice solution
That is how I solved this problem too... :)
The dotted lines in this drawing create a rectangle with area of base x height. The blue parallelogram is half of the area of that rectangle, since its height is the same and its base is 1/2. The two right triangles that remain each have an area of 1/2 base x height, so their total area equals that of the parallelogram. Now we have to show that the remaining two isosceles triangles have areas equal to that of the two right triangles. We can see that the height of these triangles is 1/2 the radius of the circle, and we know that the side of a hexagon = the radius of the circle in which it is inscribed. The base and height of the isosceles triangles are therefore equal to the height and base of the right triangles, so their areas will be the same.
If we draw a diagonal of the green parallegram, we will dividing it into two parts, each is 6 1 of the the original hexagon, thus, the area of the green part is 6 1 + 6 1 = 3 1 .
Each of the parts are actually 6 1 of the original hexagon, so the area of the green part is 3 1 that of the hexagon.
Log in to reply
Honestly, that's what I thought in the beginning but didn't find the answer so I doubted myself. I will edit my answer. Thank you.
If we draw a line to split the hexagon in half between two vertices and label the outer edge B2 and the dividing line parallel to it as B1 forming two trapezoids with height h, we can find that the total area of the hexagon is h(B1+B2). By splitting the shaded area into two congruent triangles, we can find the total shaded area to be B2h. This gives us the ratio of shaded area:total area=[B2h]/[h(B1+B2)]=B2/[B1+B2]. Since this is a regular polygon, we know that B1=2*B2 giving the ratio of 1:3.
The parallogram shaded has the same area as a rectangle. Two rectangles form the midsection and the two outer triangles are each 1/2 of a triangle. Thats a total of 3 rectangles. Therefore 1/3
Sides of the hexagon = 2.
The perpendicular of the equilateral triangles= P.
Draw the line from the middle of the bottom line on the octagon M through the center O to the middle of the top line of the octagon T.
The shaded area now is divided into two identical triangles with common properties 2p, 1, 60
, 30
Shaded area = 2( 2P * 1/2) = 2Psq
The area of the hexagon is six triangles with base 2, height P.
6( p* 2/2) = 6Psq.
I have not found how to write notation nor diagrams on the laptop I am using.
It is a simple construction
Hmm, I don't understant. What does Psq represent?
I held my finger up that best represented the colored in area and then covered the 2 un colored sides and when given the choices of coverage deduced 1/3 waa the closest to my visual estimate.....1/3 is also the amt of time it took to figure it out compared to the amt of time to type the answer.
That's a reasonable way to estimate that the answer is 1/3. But how do you know that the answer is exactly 1/3?
2x(2apx(L/2)/2)= apL, the area of the hexagon is 6Lap/2= 3Lap...... apL/3apL= 1/3
It is not clear to me what a, x, p, and L are. Could you please clarify?
VERY nice problem