Hexagon Toy Probability
The toy below is a rigid hexagon with a colored circle at each vertex. It is currently in its holder, which has corresponding colored circles at each vertex.
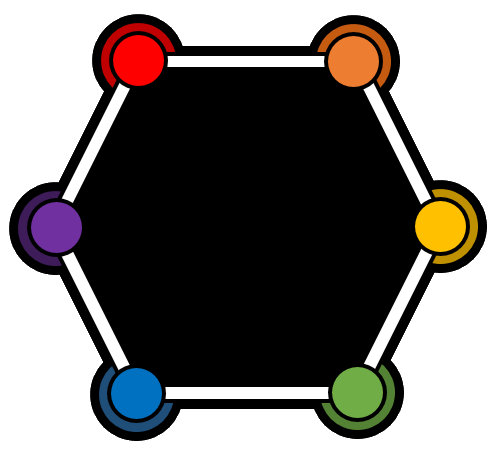
The toy is taken out of its holder, tossed around at random, and then placed back into the holder. What is the probability that the colors now match with the holder?
Note : The hexagon toy can be flipped upside down. The same colors are on the opposite side.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
Assign each vertex a number.
Starting with the red vertex of the holder and going around clockwise, the possible permutations of the toy if it does not flip upside down are:
( 1 2 3 4 5 6 ) ( 4 5 6 1 2 3 ) ( 2 3 4 5 6 1 ) ( 5 6 1 2 3 4 ) ( 3 4 5 6 1 2 ) ( 6 1 2 3 4 5 )
Starting with the red vertex of the holder and going around clockwise, the possible permutations of the toy if it does flip upside down are:
( 1 6 5 4 3 2 ) ( 4 3 2 1 6 5 ) ( 6 5 4 3 2 1 ) ( 3 2 1 6 5 4 ) ( 5 4 3 2 1 6 ) ( 2 1 6 5 4 3 )
There are 12 permutations of the toy in its holder, only one of which matches the original orientation. Therefore, the probability that the toy's colors matches its holder is 1 2 1 .