Hexagonal Albert-prism
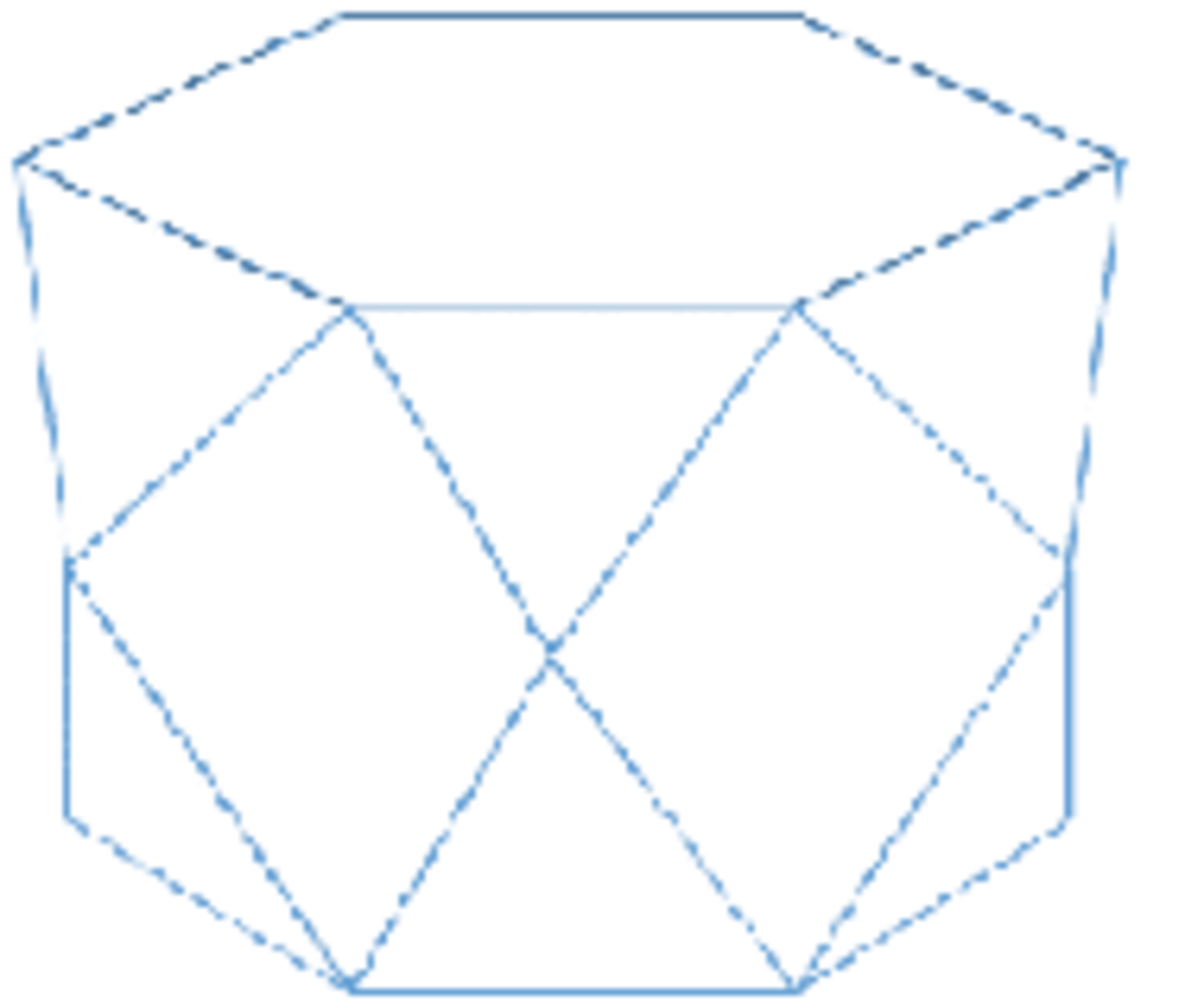
Albert was going to be famous by coming up with a new family of solids made of regular polygons. There were going to be prisms, anti-prisms, and Albert-prisms. Each Albert-prism would have two identical large regular polygons for the end faces, both attended by a row of equilateral triangles. The two rows would meet at the distant vertices and by doing would create a line square faces. However, when he tried to make a paper model of the hexagonal Albert-prism, the model kept warping.
In order for the model to work, he should have used a different quadrilateral in place of a square. Find the smallest internal angle of this quadrilateral in degrees.
Give your answer to 3 decimal places.
The answer is 70.529.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
Assuming unit sides for all the faces, A B = 2 1 . From symmetry, AC must be perpendicular to AD. Since ∠ B A D = 6 0 ∘ the foreshortened ∠ C A B = 3 0 ∘ . From the right △ A B C we get the foreshortened A C = c o s ( 3 0 ∘ ) . 5 = 3 1 . If we look at the quadrilateral face (which has to be vertical based on symmetry) head on, this is exactly the actual length of E C . The side of the quadrilateral, A C must in reality be 1. So from the right △ A E C we get the ∠ E A C = a r c s i n ( 3 1 ) = 3 5 . 2 6 4 3 9 ∘ . Doubling this will give us 7 0 . 5 2 9 ∘ .