Hexagonal Areas
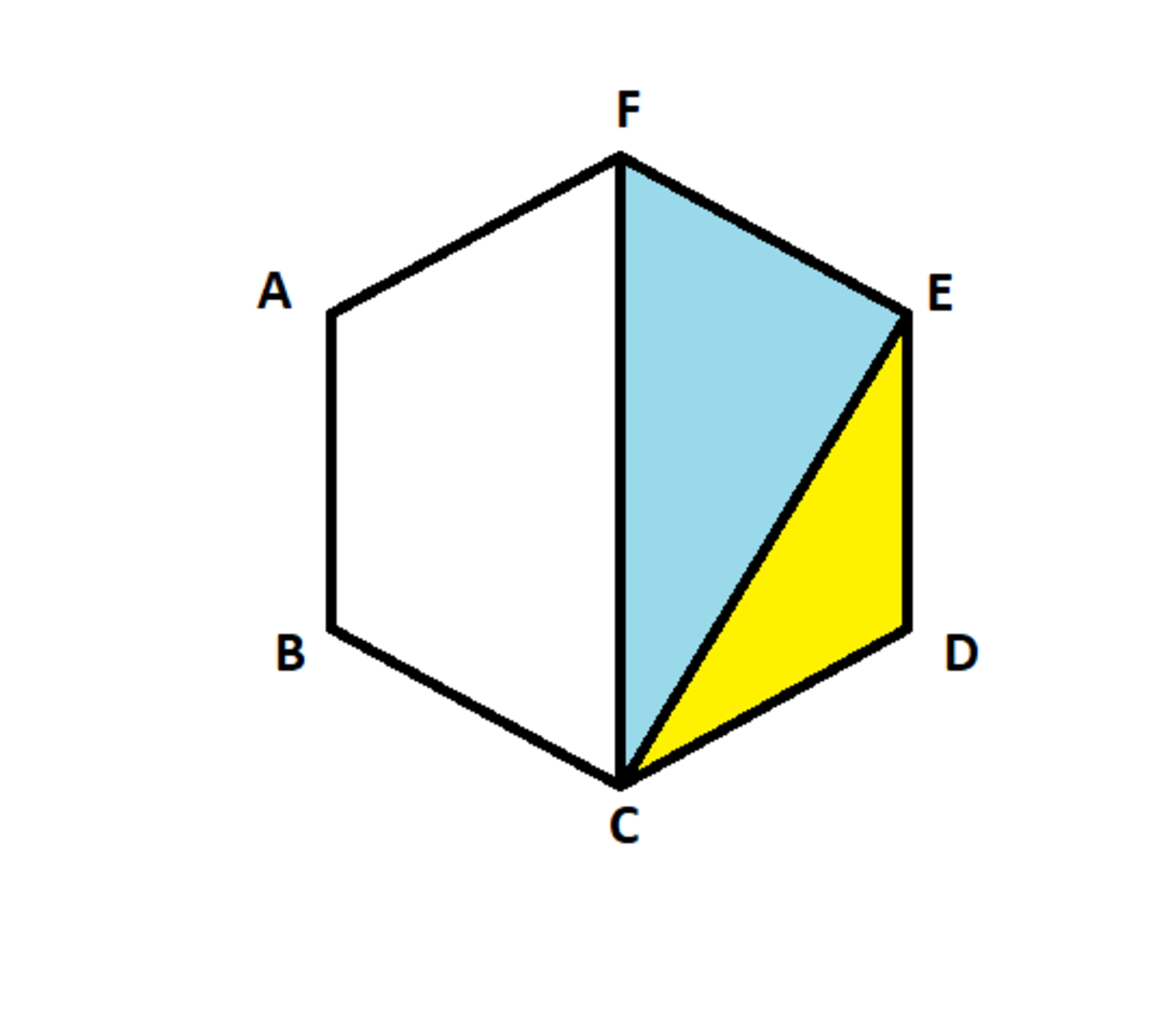
A B C D E F is a regular hexagon. Find the ratio of blue area to the yellow area. That is, find [ C D E ] [ C E F ] .
The answer is 2.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
3 solutions
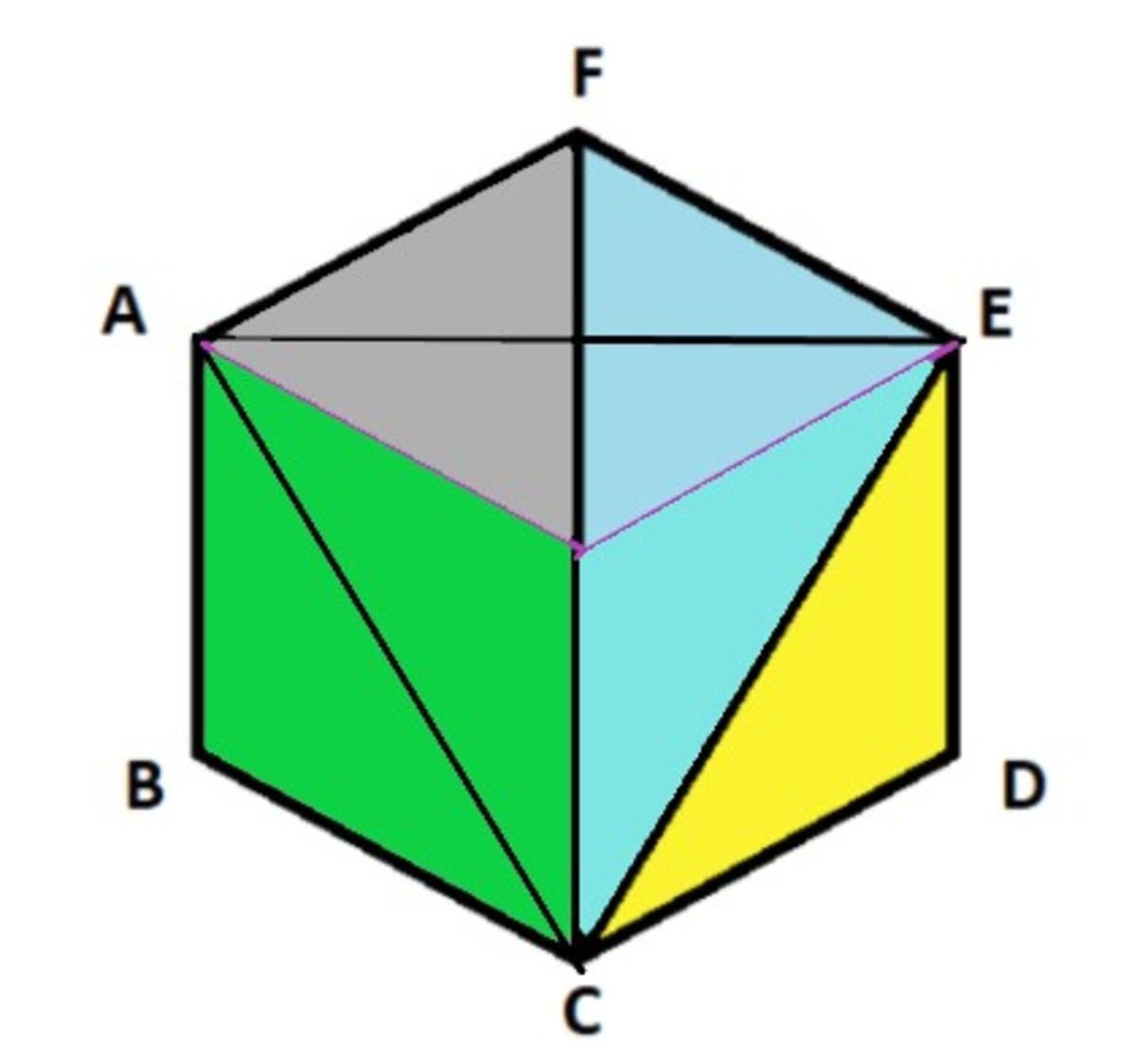
The yellow region is shared 6 1 of the total area while the blue region is shared 6 2 of total area.
Therefore, the ratio is 2 .
We note that ∠ D C E = ∠ E C F = 3 0 ∘ , and that C F = 2 C D .
We have that
[ C D E ] = 2 1 C D C E sin 3 0 ∘ , and
[ C E F ] = 2 1 C E C F sin 3 0 ∘
Dividing the second by the first, gives a ratio of 2 .
Add the following lines to make 6 congruent triangles:
There are 4 blue triangles and 2 yellow triangles, so the ratio of areas is 2 4 = 2 .