Hexagonal Bucket
A hexagonal bucket is constructed from a hexagonal base of side length 1 0 and 6 identical isosceles trapezoids as shown in the .GIF animation below. Each trapezoid has bases lengths of 1 0 and 2 0 and an altitude of 3 0 . Find the dihedral angle (in radians) between each pair of adjacent lateral (trapezoidal) faces of the bucket.
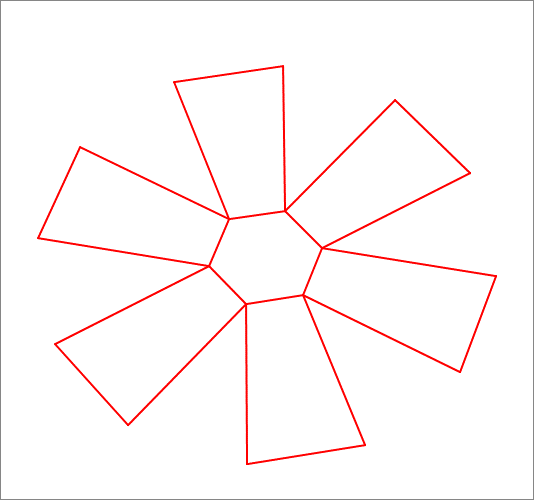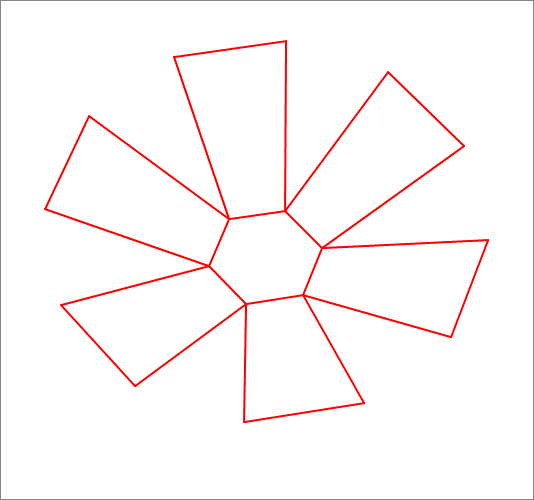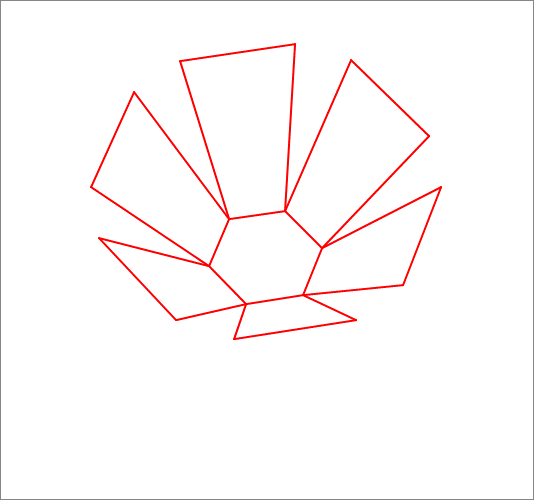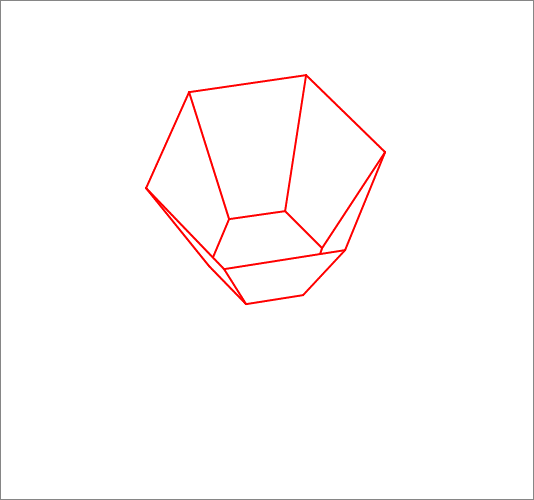
The answer is 2.143.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
4 solutions
@Mark Hennings
Sir nice solution. I just upvoted.
How this GIF's are made??
Thanks in advance.
Here is a solution with no coordinate geometry.
Toolbox:
| Pythagorean theorem |
| Triangle similarity |
| Cosine rule |
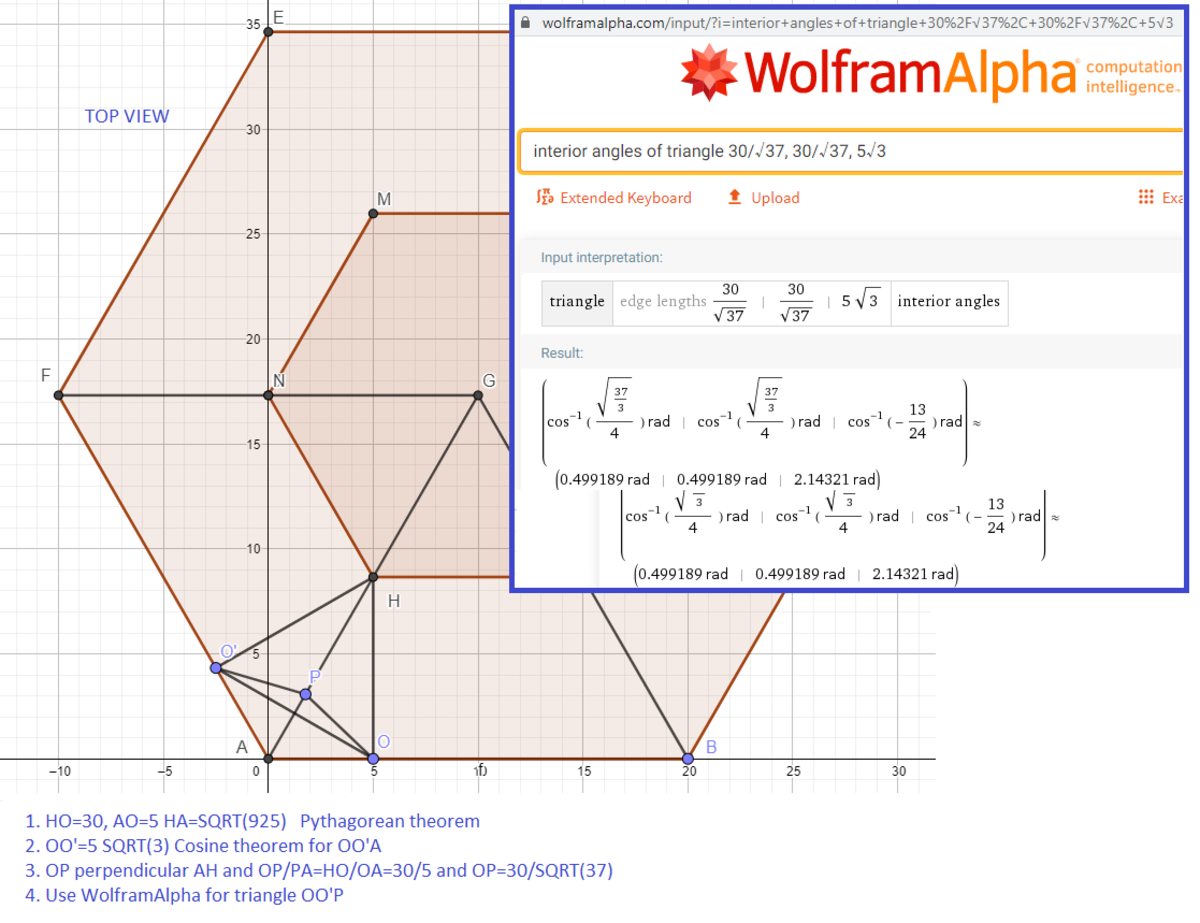
In figure 1 we have turned the bucket upside down. From vertices A and C we drop perpendiculars to edge H B (the blue line segments) creating two congruent right triangles. Hence, the perpendiculars meet at the same point M . Then the dihedral angle in question is ∠ A M C .
In order to calculate the length of A M , we isolate the face A B H G in figure 2 and split it the way David Vreken did in his solution.
By Pythagorean theorem on right triangle △ H N B we get H B = 3 0 2 + 5 2 = 5 3 7 .
Next, △ H N B and △ A M B are similar, thus, H N A M = H B A B ⇒ 3 0 A M = 5 3 7 2 0 ⇒ A M = 3 7 1 2 0
The base A B C D E F of the bucket is a regular hexagon. Hence, ∠ A B C = 3 2 π .
Using cosine rule on △ A B C , A C 2 = A B 2 + B C 2 − 2 A B ⋅ B C cos B = 2 ⋅ 2 0 2 − 2 ⋅ 2 0 2 ⋅ ( − 2 1 ) = 1 2 0 0 By cosine rule once again, this time on △ A M C ( figure 1 ), cos ( ∠ A M C ) = 2 A M ⋅ M C A M 2 + M C 2 − A C 2 = 2 ( 3 7 1 2 0 ) 2 2 ( 3 7 1 2 0 ) 2 − 1 2 0 0 = − 2 4 1 3
Hence, ∠ A M C = cos − 1 ( − 2 4 1 3 ) ≈ 2 . 1 4
Split one of the isosceles trapezoids as follows:
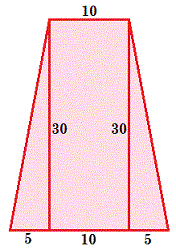
Using the Pythagorean Theorem on the right triangle with legs 5 and 3 0 , one leg of the isosceles trapezoid is 5 2 + 3 0 2 = 5 3 7 .
Now place the hexagonal bucket on a coordinate system so that the bottom center is at the origin, two vertices of the bottom hexagon are on the x -axis, and the center of the top hexagon is on the z -axis, and label the points as follows:
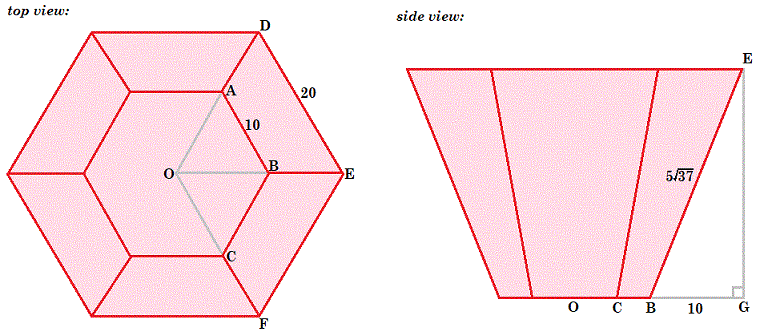
Since the difference of the hexagons along the x -axis is B G = 2 0 − 1 0 = 1 0 , and since the leg of an isosceles trapezoid is B E = 5 3 7 , then by the Pythagorean Theorem on △ B E G the height of the bucket is E G = ( 5 3 7 ) 2 − 1 0 2 = 5 3 3 . Using the properties of equilateral triangles, the coordinates for A , B , C , and E are then A ( 5 , 5 3 , 0 ) , B ( 1 0 , 0 , 0 ) , C ( 5 , − 5 3 , 0 ) , and E ( 2 0 , 0 , 5 3 3 ) .
The equation of the plane with A , B , and E is in the form of x + b y + c z = d . Using the coordinates for A , B , and E gives equations 5 + 5 3 b = d , 1 0 = d , and 2 0 + 5 3 3 c = d , which solve to b = 3 3 , c = − 3 3 2 3 3 , and d = 1 0 , for a planar equation of x + 3 3 y − 3 3 2 3 3 z = 1 0 , which is equivalent to 3 3 x + 1 1 3 y − 2 3 3 z = 3 3 0 . By a similar argument, the equation of the plane through B , C , and E is 3 3 x − 1 1 3 y − 2 3 3 z = 3 3 0 .
The acute angle between the two planar equations is θ = cos − 1 ( ( 3 3 ) 2 + ( 1 1 3 ) 2 + ( − 2 3 3 ) 2 ( 3 3 ) 2 + ( − 1 1 3 ) 2 + ( − 2 3 3 ) 2 ( 3 3 ) ( 3 3 ) + ( 1 1 3 ) ( − 1 1 3 ) + ( − 2 3 3 ) ( − 2 3 3 ) ) = cos − 1 ( 2 4 1 3 ) , so the obtuse angle (the angle that we want) is π − θ = π − cos − 1 ( 2 4 1 3 ) ≈ 2 . 1 4 3 .
Thank you for a well-explained solution.
Using David's labelling, A , B , C have coordinates ( 5 , 5 3 , 0 ) , ( 1 0 , 0 , 0 ) , and ( 5 , − 5 3 , 0 ) respectively, while D , E , F have coordinates ( 1 0 , 1 0 3 , h ) , ( 2 0 , 0 , h ) and ( 1 0 , − 1 0 3 , h ) respectively, where h is the vertical height of the basket. Planes A B E D and B C F E have respective normal vectors n 1 = B E × A D = ⎝ ⎛ − 5 h 3 − 5 h 5 0 3 ⎠ ⎞ n 2 = C F × B E = ⎝ ⎛ − 5 h 3 5 h 5 0 3 ⎠ ⎞ and hence n 1 ⋅ n 2 = 5 0 ( h 2 + 1 5 0 ) ∣ n 1 ∣ 2 = ∣ n 2 ∣ 2 = 5 0 ( 2 h 2 + 1 5 0 ) Thus, if θ is the acute angle between two adjacent trapezia (UK terminology), then cos θ = 2 h 2 + 1 5 0 h 2 + 1 5 0 Now h 2 + 1 0 2 = ∣ B E ∣ 2 = 3 0 2 + 5 2 , and hence h 2 = 8 2 5 , and hence cos θ = 2 4 1 3 . Thus the dihedral angle between the two trapezia is π − θ = 2 . 1 4 3 2 1 4 8 9 9 .