Hexagonal Checkers
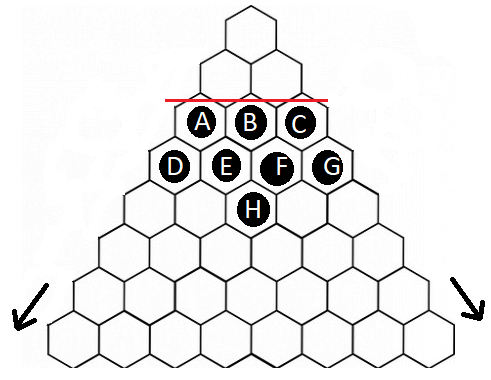
Consider an infinitely large triangle constructed out of hexagons. We will play a mathematical version of checkers on this board. To start, we place any number of checkers below a given line. Our goal is then to get checkers into the top three spaces on the board through a series of moves. A move, as in regular checkers, consists of a checker jumping over an adjacent checker, which eliminates the checker which was jumped over. It is possible to get checkers into the top three spaces when the line is just below the second row. One possible way to do this is to use the starting configuration below and move checkers D, E, C, H, and G, respectively.
What is the largest possible such that we can get checkers into the top three spaces when the line is below the row?
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
To start, we place the number r n − 1 into each cell, where n is the row that the cell is in and r = 2 5 − 1 . We then define the characteristic value of each state of the game to be the sum of all the cells that have a checker on them. Notice that for each move, the characteristic value either stays the same or decreases (this is true because r 2 + r = 1 . In other words the characteristic value at the beginning of a game will be greater than or equal to the characteristic value at the end of the game. The characteristic value of the desired state (checkers in the top three cells) is 5 ≈ 2 . 2 3 6 We notice by the formula for the arithmetico-geometric sequence that the characteristic value for a checkerboard with all the cells filled would be 2 7 + 3 5 ≈ 6 . 8 5 4 If the line were below the fifth row, the maximum possible characteristic value for the beginning state would be 2 − 2 1 + 1 1 5 ≈ 1 . 7 9 8 Therefore it is impossible to get checkers into the top three cells when n = 5 . The n = 4 case can be shown by example.
Note: Unfortunately, when I found the n = 4 case by hand, it took me too many moves to be short enough to share here. If you would like to verify the n = 4 case for yourself please go ahead and do so. I would recommend finding the solution backwards (i.e. starting with the top three cells filled and replacing one checker with two checkers in the appropriate manner until you get all checkers below the fourth row). Also, if you find it easier, you can notice that the game on a hexagonal grid is equivalent to the game on one quadrant of a square grid.