Hexagonal Numbers
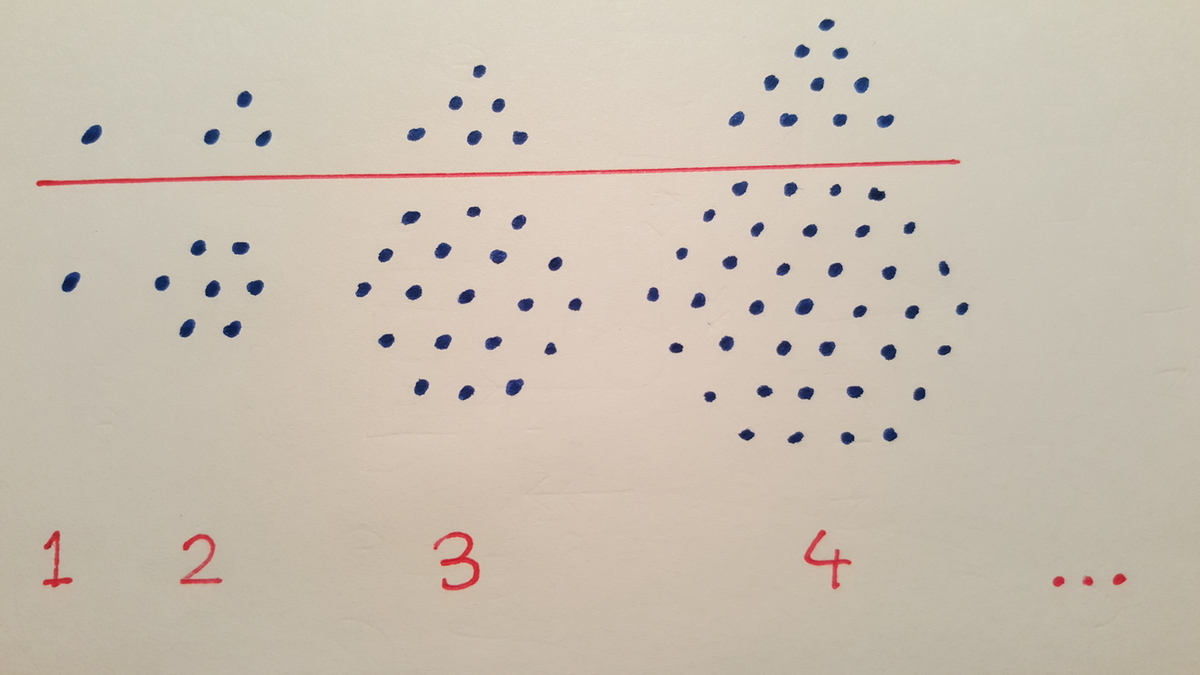
In the diagram above, we see a series of triangles and hexagons. How many dots are contained in the 2 0 th hexagon?
The answer is 1141.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
6 solutions
Great question! :)
Log in to reply
Except that the question lies. It says the hexagons represent hexagonal numbers, but hexagonal numbers are represented by outlines only, and the nth hexagonal number is the total dots of each outline from 1 to n-sided hexagons when they're overlapped to share one vertex.
https://en.m.wikipedia.org/wiki/Hexagonal_number
1141 is the correct answer to the actual question but the question needs to not say they represent hexagonal numbers since that will mislead people to the wrong equation to use.
We can deduce that each two consecutive hexagonal number has a difference which follows an arithmetic sequence - +6,+12,+18......
Which is apparently an AP with a first term 6 ,general difference(difference of difference)6,and term number 19.
So we can directly get the solution :1+1140(By using AP sum formula)=1141
In my case, I notice that I can use AP (Arithmetic Progression) for this question. As you can see, in every increase in number, the hexagon increase 1 outer layer. And since it is an hexagon, so it is an increment of 6. From here I could generate an AP formula.
According to AP formula, an=a1+(n-1)d. Sn=n(a1+an)/2. I let a1 = 6 which is the first increment of hexagon. d = 6, which is increment of every hexagon. and n = 19 for the 20th hexagon.
First I need to find how many dots are in the 20th hexagon. So a19=6+(19-1)6 and I get 114. And after I have the a19 value, I find the sum. S19=19(6+114)/2 which is equal to 1140. Never forgot the 1 miserable dot in the center.
And that's how I got the answer.
i found that n th hexagonal no. was of the form n 3 − ( n − 1 ) 3 .
2 0 3 − 1 9 3 = 1 1 4 1
Can you tell us why that's the case?
In first figure , there is only
1
dot.
In second figure, there are
2
+
3
+
2
dots.
In third figure, there are
3
+
4
+
5
+
4
+
3
dots.
In fourth figure, there are
4
+
5
+
6
+
7
+
6
+
5
+
4
dots.
So, we see that in each case the number of dots in the
n
t
h
hexagon, is
n
+
[
n
+
1
]
+
[
n
+
2
]
+
⋯
+
[
2
n
−
1
]
+
[
2
n
−
2
]
+
⋯
+
[
n
+
1
]
+
n
dots.
So, in the
2
0
t
h
hexagon, the number of dots are
2
0
+
2
1
+
⋯
+
3
9
+
3
8
+
⋯
+
2
1
+
2
0
dots.
=
[
[
2
×
2
3
9
×
4
0
]
−
3
9
]
−
[
2
×
[
2
1
9
×
2
0
]
]
=
[
(
3
9
×
4
0
)
−
3
9
]
−
[
1
9
×
2
0
]
=
[
1
5
6
0
−
3
9
]
−
[
3
8
0
]
=
1
5
2
1
−
3
8
0
=
1
1
4
1
Moderator note:
Good explanation for how to count the dots in the pattern, by splitting it up into 2 sequences that we easily understand.
The median line which divides the hexagon in two halfs follows an aritmetic progression (1,3,5,7...). Therefore, the 20º term can be calculated as follows: an=a1+(n-1).r--> a20=1+19.2=39. That median line acts like a mirror, thereby the same amount of dots are found above and below it. Whatever direction you look from this parameter, you must found another aritmetic progression (38, 37, 36, .... , 20). The sum of its elements is: S=(a1+an).n/2---> S=(20+38).19/2=58.19/2=29.19=551. Since we have two of this A.P.s: 2.551=1102. Now, one just must add the amount of dots of the median line (39): 1102+39=1141.
I've added to each hexagon six 'petals'. As we can see, for the n t h hexagon, these petals grow just like triangular numbers of size n − 1 . We know the formula for the n t h triangular number is 2 1 n ( n + 1 ) , so we substitute n for ( n − 1 ) to get 2 1 n ( n − 1 ) . We have 6 of these petals plus the one central dot, which gives 1 + 3 n ( n − 1 ) . Putting n = 2 0 into this formula yields 1 1 4 1