Hexagonal Ohm
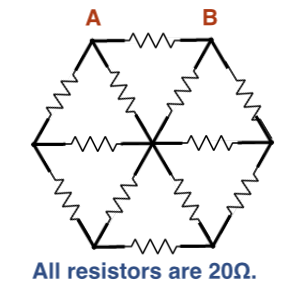
Twelve identical wires are connected in the plane as shown in the figure above. The six outer wires make a regular hexagon and the remaining six join the vertices of this hexagon with the hexagon's center. Each wire has a resistance of . Calculate effective resistance between and .
The answer is 11.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
Using the principles of Thevenin equivalent resistance a circuit or part of a circuit, that contains only resistors, can be replaced by a single resistance value. By breaking the circuit down into smaller parts and then using the calculated Thevenin equivalent resistance in subsequent calculations the total equivalent resistance can be determined.
- - denotes series.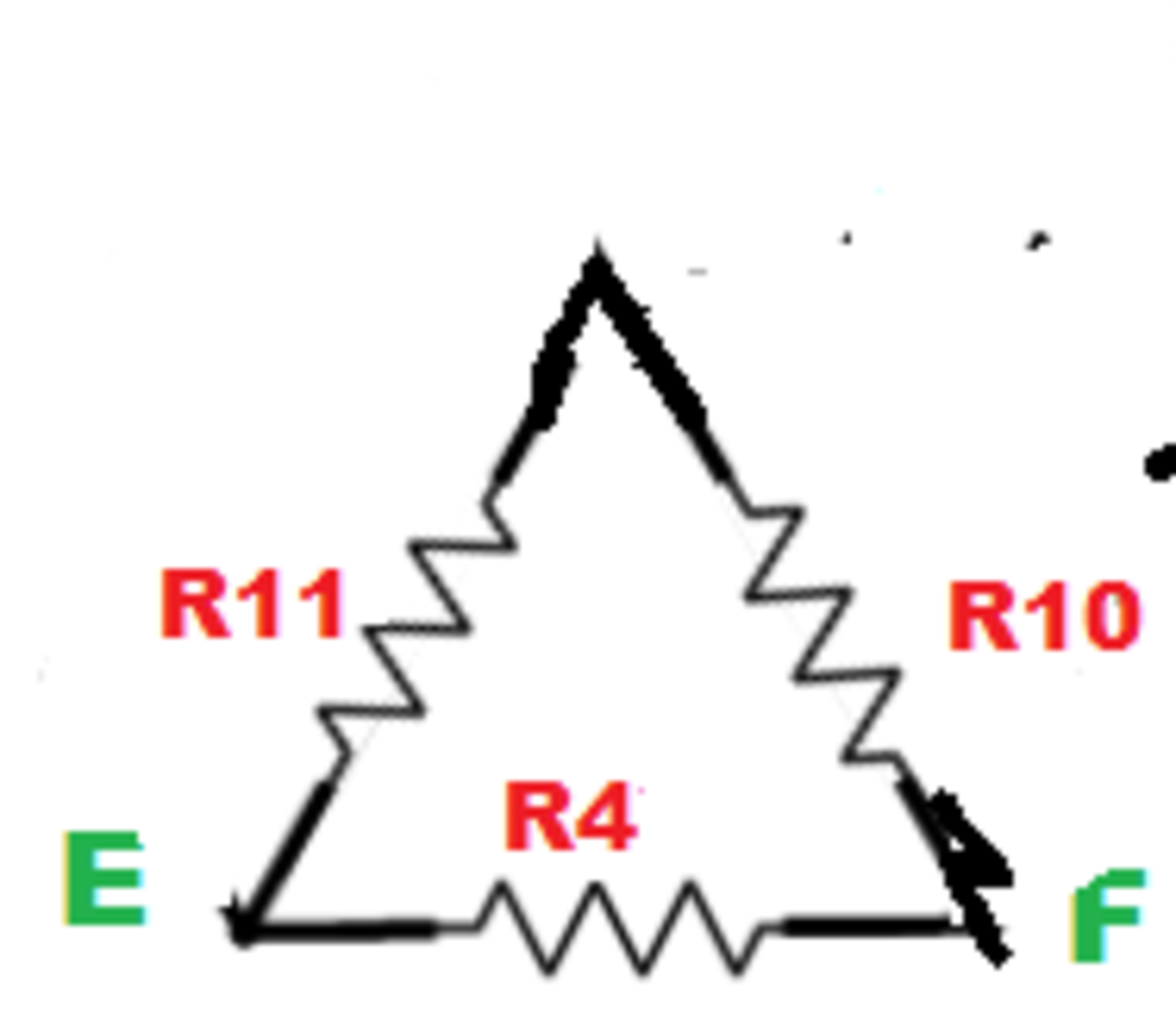 Calculating the equivalent resistance R,EF considering only the resistors R4, R10, R11.
Calculating the equivalent resistance R,EF considering only the resistors R4, R10, R11.
R,EF = (R11 - - R10) || R4
R E F 1 = R 1 1 + R 1 0 1 + R 4 1 = 4 0 1 + 2 0 1 = 4 0 3
R E F = 3 4 0 Ω
R,CD = (R12 - - R9 || (R3 - - REF - - R5).
R C D 1 = R 1 2 + R 9 1 + R 3 + R E F + R 5 1 = 2 0 + 2 0 1 + 2 0 + 3 4 0 + 2 0 1 = 4 0 1 + 1 6 0 3 = 1 6 0 7
R C D = 7 1 6 0 Ω
Calculating the equivalent resistance, R,AB considering the resistances R1, R2, R6, R7, R8, R,CD.
R,AB = R1 || (R7 - - R8) || (R2 - - R,CD - - R6) R A B 1 = R 1 1 + R 7 + R 8 1 + R 2 + R C D + R 6 1 = 2 0 1 + 4 0 1 + 2 0 + 7 1 6 0 + 2 0 1 = 4 4 0 4 0
R A B = 1 1 Ω