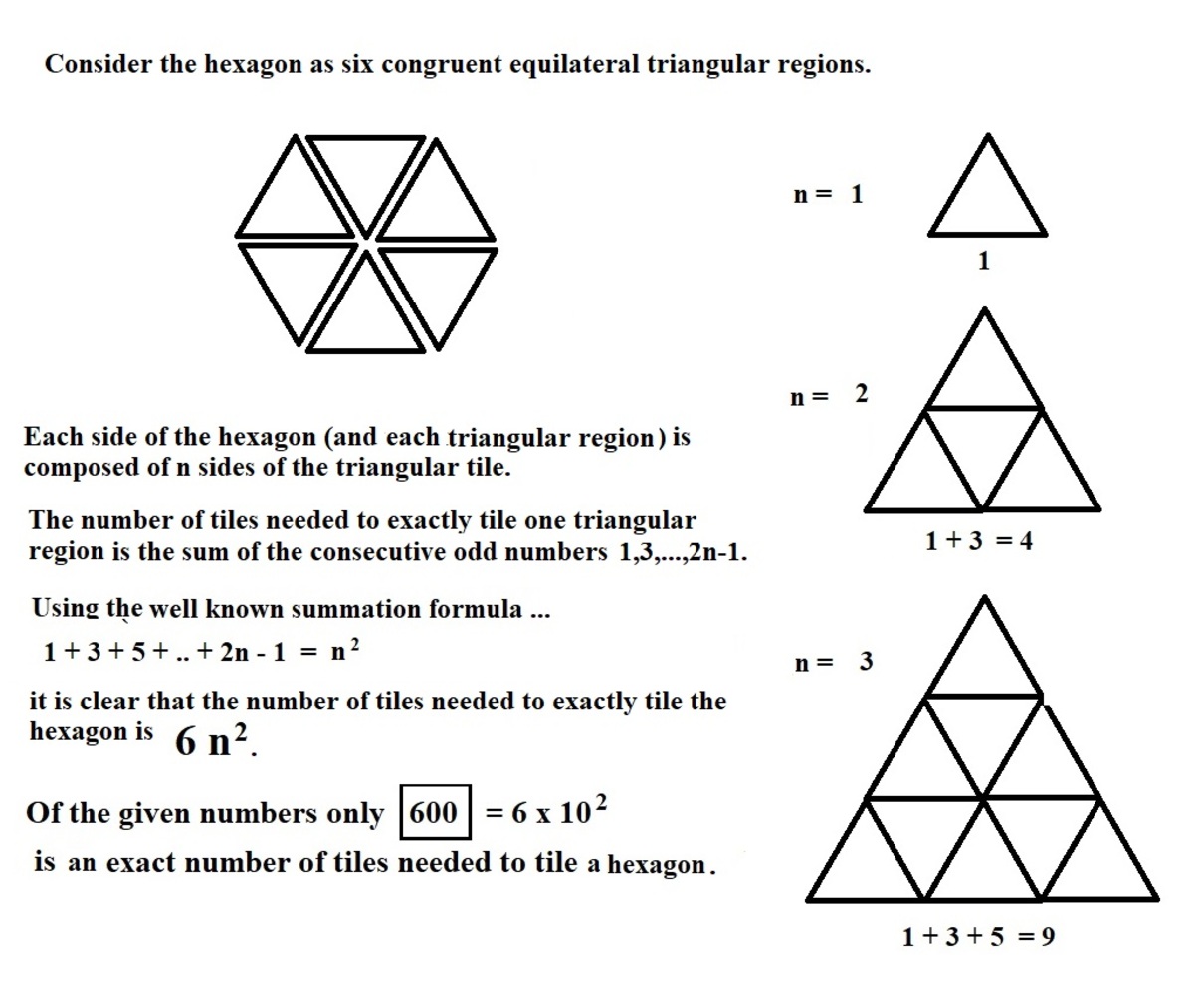
Hexagonal Tilings with Triangular Tiles
The diagram shows how identical equilateral triangles can be tiled to make a regular hexagon with no leftover tiles .
Which of the following numbers of triangles can also do this?
Regular hexagons can be made with 6 tiles, 24 tiles, and 54 tiles.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
29 solutions
Moderator note:
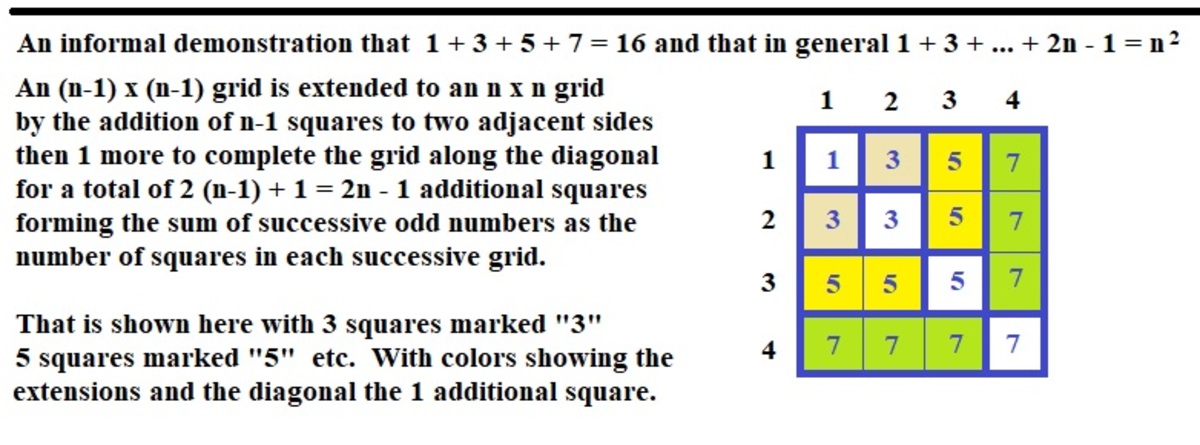
The question came up in the comments how we know the sum of odd numbers is a square number. Answering this question (from the introduction to our Algebra Through Puzzles course) should help:
Wow, this is a pretty nice way to figure out the general value
Log in to reply
It goes to 2n-1, not 2n-1 squared, otherwise, fine
Clever way of thinking...
where did you get that (2n-1)? and how does it become n^2? newbie
Log in to reply
Check the link I added to the moderator note in this solution.
I have no idea where I miscalculated to get 540 I just recalculated my function and got 600. Should have double checked before submitting
I liked your idea its pretty cool
Sum of odd numbers is n^2 + 2n. Hence answer would be 720.
Log in to reply
Actually, your formula is for the sum of the first n integers, not the sum of the first n odd integers.
Relevant wiki: Sum of n, n², or n³
If we denote E n to be the number of equilateral triangles needed to form regular hexagon with side length n (we take side of small equilateral as a unit of measure), we can write recurrence relation: E n = E n − 1 + 6 ( 2 n − 1 ) . Now, since E 0 = 0 , we have: E n = k = 1 ∑ n 6 ( 2 k − 1 ) = 1 2 k = 1 ∑ n k − 6 k = 1 ∑ n 1 = 1 2 ⋅ 2 n ( n + 1 ) − 6 n = 6 n 2 The only number of this form given is 6 0 0 .
How did you get from line 3 to line 4?
Log in to reply
What lines exactly are you referring to?
Log in to reply
On the equation there are 4 phases, each is called a line (I guess). Edit: I don't understand those things, so for the rest, lets hope for someone else to answer... :'D
Relevant wiki: Method of Differences
Working out the next in the sequence gives a total of 96 triangles used. The sequence of tiles required to form each hexagon is therefore as follows: 6, 24, 54, 96, ... If we work out the nth term for this quadratic sequence:
Sequence: 6, 24, 54, 96, ...
First difference: 18, 30, 42, ...
Second difference: 12, 12, ... ( 2 1 2 = 6: the coefficient of n²)
(Since the second difference is constant, the sequence is quadratic.)
n²: 1, 4, 9, 25, ...
6n²: 6, 24, 54, 96, ... (the coefficient of n² is 6)
which is equal to the sequence so the nth term of the sequence is 6n². Since 600 is the only option divisible by 6 which gives a square number (600 / 6 =100 = 10²) (which is necessary for 6n² to be a whole number), then 600 must be the answer.
How did you 10 and why did you do 12/2?
Log in to reply
In this method of finding the nth term of a quadratic sequence, you always divide the second difference (if it is constant and therefore a quadratic sequence) by 2. The reason why is because any quadratic is in the form: ax²+bx+c. let n be a value of x in the sequence so the nth term is an²+bn+c. The (n+1)th term = a(n+1)² + b(n+1)+c = a(n²+2n+1)+bn+b+c = an²+2an+a+bn+b+c. The first difference between these two terms is (an²+2an+a+bn+b+c)-(an²+bn+c) = 2an+a+b. The (n+2)th term = a(n+2)²+b(n+2)+c = a(n²+4n+4)+bn+2b+c = an²+4an+4a+bn+2b+c. The first difference between the (n+1)th term and the (n+2)th term is (an²+4an+4a+bn+2b+c)-(an²+2an+a+bn+b+c) = 2an+3a+b. The second difference is therefore: (2an+3a+b)-(2an+a+b) = 2a therefore the second difference is 2 X a (where a was the coefficient of x². In short the reason why you divide by 2 (and 12/2 was what I did above) is because the second difference between square numbers is always 2 (e.g. 4-1=3; 9-4=5; second difference: 5-3=2). Therefore, to cancel this out, we must divide by 2. I hope that makes sense and clears things up.
Every Hexagon can be divided into 6 big triangles. Each triangle is the same and is further divided into a number of small triangles. This further division into small equilateral triangles follows a pattern of 1, 4, 9, 16 . . . So, we know, that the * total number of little triangles is a multiple of 6 and a perfect square. * All the answers are divisible by 6 but only 1 answer leaves a perfect square i.e. 100.
It could be a Quadratic Function... Let S(n) be the number of equilateral triangle in a hexagon with n triangles for each side...
S(n)=an^2 + bn + c
6=a+b+c 24=4a+2b+c 54=9a+3b+c
Solve using systems: We will get a=6, b=0, and c=0
So: S(n)=6n^2
Let n=10 S(10)=6(10^2)=600
So 600
600 is the only answer divisible by 6
Moderator note:
Just to note, for featuring this problem on Problem of the Week we have modified the multiple choice so this solution doesn't work any more.
Is that a sufficient condition?
Log in to reply
Zico has given a much more complete answer. The number has to be of the form 6 n 2 .
Thanks, now it's a much better problem.
No its not. It is still divisible from 720 720÷6=120.
Log in to reply
All the option choices are divisible by six. So the divisibility test won't work.
now that's better!
Um... they're all divisible by 6 guy...
First its 6, then 18 triangles are added with total of 24, then 30 are added with a total of 54 and so on... 6.1 + 6.3 + 6.5 +.... We can see that this is a series, just keep on adding successive numbers until you get one of the four numbers!
1st Hexagon = 6 Equilateral triangles = 6x 1 2 2nd Hexagon = 24 Equilateral triangles = 6x 2 2 3rd Hexagon = 54 Equilateral triangles = 6x 3 2
It can be conjectured that the number of hexagons = 6 n 2 . 600 is the only number given which is 6x(a square).
The sequence is as 6, 24 , 54 ...
Which can be broken down as 6, 6 + 6×3 , 6 +6×3 +6×5, .....
So for the the nth sequence that would up to requisite no. of triangle
N th = 6 + 6×3 +6×5 + ..... 6× n
= 6( 1 +3 +5 ...+ n)
=6{ (n/2)×(2×1 + (n-1)×2)}
= 6n^2
And the only option that gives the perfect square on dividing by 6 is 600
Notice that the first phase has 6 1 triangles, the 2nd phase has 6 3 triangles, and added up together give us 6 4 triangles. And this is true because is easy to see that when we look up the following phase there is always 12 more triangles (6 2) this means that the number of triangles at the n th phase is 6(2n-1), because the phases are always growing in pairs (so we know that the next phase is just the previous one plus 6*2). But we are not supposed to calculate the number of triangles at one phase, we were asked for calculating the sum of the phases. Since the triangles of a phase n is defined by an odd number, and the sum of n phases must be defined by the sum of every single odd number from 1 to 2n-1. This can also be expressed as n². It's a very common example when teaching proof by induction (since it's true for n=1, we suppose that the statement is true for n=k, and then prove that it holds for n=k+1. If that's true, it will hold for all the positive integer values due to the fact, 2 is 1+1, and 3 is 2+1, etc.). So we can express the sum of n phases as 6n² and try to substitute the values purposed below. If it's a valid number, n will be an integer. The only number which matches is 600.
Tiles increase as follows: 6(1) 6(1+3) 6(1+3+5) In general six times an odd number summation. Since: 1+3+5+...+kth_odd = k^2 All options are divisible by 6, but only √100 gives an integer, only 600 can be a number of tiles.
Count Triangles: N1=6 N2= 6+18=24 N3=6+18+30=54
All have common factor 6: N1=6•1 N2=6•4 N3=6•9
General Form: Ni=6•i^2 Or Ni/6=Ni^2
The only answer when divided by 6 that results in a perfect square is 600. 600/6=100=10^2; i=10.
Since the question of the sum of consecutive odd integers being a perfect square was raised elsewhere .....
We start with a hexagon with an outer layer of 6 triangles. Adding 12 gives one with an outer layer of 18 triangles, then 30, etc. The total number of triangles in each hexagon is equal to its predecessor plus the number of triangles on the outer layer. This means our sums will be 6, (6 + 18), (6 + 18 + 30), etc. Eventually, such a pattern gives a total of 600, which is the correct answer.
In an Excel spreadsheet, place the series of odd number 3, 5, 7... in column A starting at cell A2. Place the number 6 in cell B1. In cell B2, place the formula =B1+(A2*6). Drag this formula down column B for as may cells as you have filled in column A. This will compute the number of triangles required for successively larger hexagons.
2×3=6 4×6=24 6×9=54 ..... .. ..... 20×30=600 it follows the same pattern that's all I know
Triangle must be made of perfect square amount of equilateral triangles. The first triangle has 1 the next has 4 then the next triangle has 9 and so on. You need 6 of those triangles to make a regular triangle. Dividing all of the solutions by 6 we see 600 / 6 = 100 which is the only perfect square and can therefore make a subtriangle.
We can note that the number of triangles to make one side of the hexagon is a perfect square (c.f. table below).
| Number of triangles | Number of triangles by side |
| 6 = 6 ⋅ 1 | 1 |
| 2 4 = 6 ⋅ ( 1 + 3 ) | 4 |
| 5 4 = 6 ⋅ ( 1 + 3 + 5 ) | 9 |
In general, if we have N interactions so we have N 2 triangles by side. Then, with we have a number n , just divide n by 6 and if the result is a perfect square so we can make a regular hexagon. We can see that 6 0 0 / 6 = 1 0 0 and 1 0 0 is a perfect square soon we can build a regular hexagon.
"Algorithm" in c++ for(int i = 1; i < 800; i+=2){ x+=i*6; cout<<x<<' '; }
The number of tiles can be treated as a sequence: 6, 24, 54. When I divided each by it's greatest common factor, I got another amazing sequence: 1, 4, 9 - the first three integers squared. This makes the sequence: ∑ n = 1 ∞ 6 n 2
Number of tiles, T=6+3.6+5.6+7.6+9.6+.............+(2n-1).6 =6[1+3+5+7+.........+(2n-1)]=6*S(suppose the series of n odd numbers=S) Now we need to calculate S= [1+3+5+7+.......+(2n-1)]
S=1+3+5+7+.....(2n-3)+(2n-1)...............(1) S=(2n-1)+(2n-3)+.....+3+1...............(2) By adding (1) and (2)- 2S=n.2n S=n^2 So we got number of tiles T=6*n^2 here we should get a natural number for n. From the options only 600 gives us a natural number for n. Because 600/6=100 is a square of 10. So we can get n=10. So the answer is 600.
Using Progressions, we can solve the question.
Sequence of number of triangles in each layer: 6, 18, 30, ... Starting term, a = 6 Common difference, d = 18 - 6 = 12
To get the total number of triangles, we sum up the sequence of number of triangles in each layer using the formula Sn = n/2 (2a + (n - 1) d). Therefore, Sn = n/2 (2(6) + (n - 1) 12) = 6n^2
Then set 6n^2 equal to the options that are given. If n is an integer, that is the answer. 6n^2 = 600 n^2 = 100 n = 10
6(n)^2 = number of triangles in reg hexagon; 1=6, 2=24,3=54 etc... 10=600
6,24,54,96,150,216,294,384,486,600...
If you take a look at the example you will notice that the number of triangles needed to make a regular hexagon of any size is 6 x n, where n is a square number. As shown in the example, 6 x 1 = 6, 6 x 4 = 24 and 6 x 9 = 54 (1, 4 and 9 are square numbers). The only option where 6 is multiplied by a square number is 600, which is 6 x 100.
Just get the numbers from 1 to 10 squared and multiple them by the base 6.
The pattern is 6 × n squared To check the numbers you divide them by six and look if the square root results in an integer.
The amount of tiles is 6 times a triangular number, i.e. a number of the form 1 + 3 + 5 + . . . + ( 2 n − 1 ) = n 2 . Only 600 has this property: 6 0 0 = 6 ∗ 1 0 2
Sum of triangles is = 6 (1) + 6 (3) + 6 (5) ...........+ 6 (1+2(n-1))
So it is concluded that the sum of the triangles divided by 6 must be the sum of the following arithmetic sequence: 1,3,5,.......(2n-1)
Which is equivalent to (n/2)(2a+(n-1)d) where d=2 and a=1, so the sum is n^2 , in other words it must be a square number.
The only square number in the above options is 600/6=100
Every time the outer layer will consist of the number of triangles= 6 odd. So for first its 6 1, for second total triangles will be 6+6x3=24, for third it will be 24+6x5=54 and so on we can write the function as f(n)=f(n-1) + 6x(2xn-1) where f(0) =0.
Relevant wiki: General Term Pattern Recognition