Hexed Hex

$\angle A + \angle C + \angle E = 360$ . Therefore point A reflected about BF will produce point O, circumcenter of $\triangle BDF$ . Same point $O$ will be produced by reflection of point C about BD and point E about DF.

By inscribed angle theorem $\angle FDB = 100/2=50$ .

$\angle FDE = (180-138)/2=21$

$\angle BDC = (180-122)/2=29$

$\angle CDE= \angle FDB+\angle FDE+ \angle BDC= 50 + 21+29= \boxed{100}$

Another way to solve it is to look at the hexagon as three adjacent rhombuses: ABOF, BCDO, DEFO. $\angle ODE = 180-138=42$ , $\angle ODC = 180-122=58 \Rightarrow \angle EDC = 42+58= \boxed{100}$ .

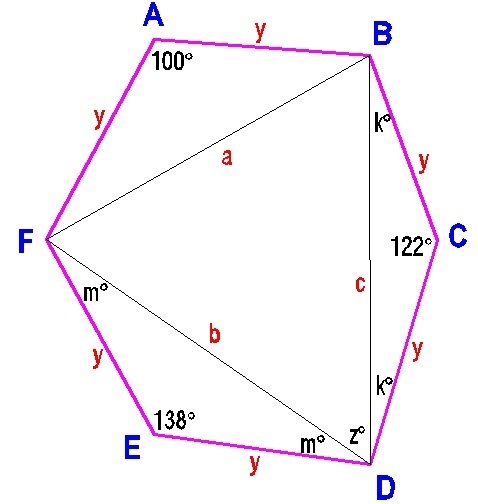By Law of Cosines

$a^2 = 2y^2 - 2y^2cos100 = y^2(2 - 2cos100)$

$a = y\sqrt{2 - 2cos100}$

$b^2 = y^2(2 - 2cos138$

$b = y\sqrt{2 - 2cos138}$

$c^2 = y^2(2 - 2cos122)$

$c = y\sqrt{2 - 2cos122}$

Solving for $m$ ,

$y^2 = y^2 + b^2 - 2(y)(b)cosm$

$m = 21$

Solving for $k$ ,

$y^2 = y^2 + c^2 - 2(y)(c)cosk$

$k = 29$

Solving for $z$ ,

$a^2 = b^2 + c^2 - 2(b)(c)cosz$

$z = 50$

$\angle CDE = 21 + 29 + 50 = 100$

Angle $x=\angle EDF+\angle FDB+\angle BDC$ .

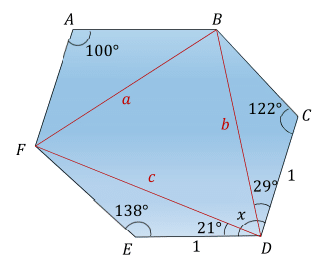
Angle $EDF=\frac{1}{2}(180^\circ-138^\circ)=21^\circ$ from the isosceles triangle $EDF$ .

Angle $BDC=\frac{1}{2}(180^\circ-122^\circ)=29^\circ$ from the isosceles triangle $BDC$ .

To get angle $FDB$ we will use the triangle $FDB$ , after we find its sides $a, b$ and $c$ using the law of cosines and the arbitrary assumption that every side of the hexagon is size 1.

$a=\sqrt{2-2cos(100)}=1.532$

$b=\sqrt{2-2cos(122)}=1.749$

$c=\sqrt{2-2cos(138)}=1.867$

One more use of the law of cosines, this time in reverse, will give us

$\angle FDB=arccos(\frac{b^2+c^2-a^2}{2bc})=50^\circ$

$x=\angle EDF+\angle FDB+\angle BDC=21^\circ+50^\circ+29^\circ=100^\circ$