Hexy Circles
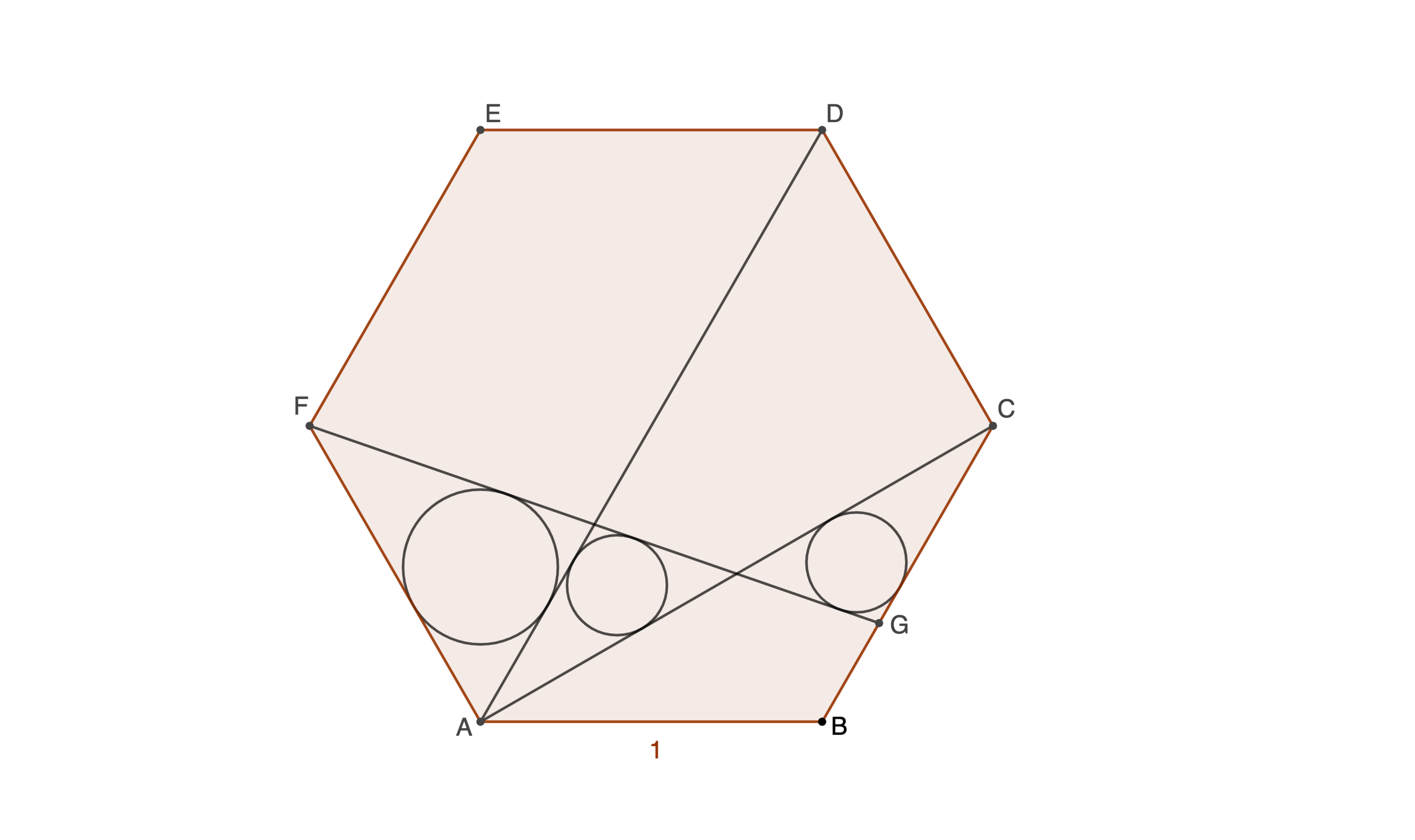
is one side of a regular hexagon. It has length 1. is chosen so that the two small circles are congruent. If the radius, , of the larger circle is , where are co-prime positive integers and are square-free, submit .
The answer is 21.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
Answer
= 5 + 7 + 6 + 3
= 21
Extrapolated FG will meet extrapolated AB at the same point AB meets DC (by congruent triangles from congruent incircles). Let this point be X. AB = BX = 1 so AX = 2. If we put an equilateral triangle of side 2 under the hexagon with one of its edge being AX, it will be a similar triangle to the one containing the big incircle which radius we're looking for with resizing factor of 3. Obviously the sides of this big triangle are 2 and 3, and the other side of √7 can be found using the angle of 60°.