Hey, they look like my teeth
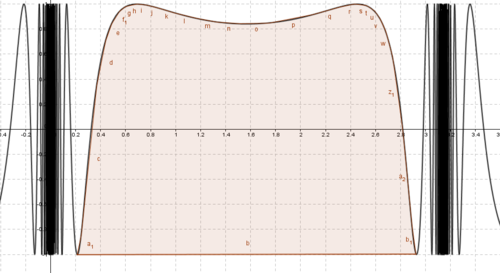 The plot of the function
The plot of the function
has a resemblance of the picture. Find the area of the 'molar' to 2 decimal places.
The answer is 4.73.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
We'll have to find the lowest points of the "molar" plot, and we can do so by differentiation:
f ′ ( x ) = − cos ( x ) ∗ ( cos ( 1 / sin x ) ) / ( sin x ) 2 = 0
There are many values that give f'(x) = 0, but the 2 corresponding coordinates to the figure are (0.2138, -1) and (2.9278, -1).
If we set a new function g(x) = \sin(\csc(x))+1, the "molar" will rise above the x-axis, and we can simply calculate the area by using definite integral from 0.2138 to 2.9278:
So the area is roughly 4.74.