This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
3 solutions
@Chew-Seong Cheong , can I know what program you used to draw these geometric figures?
Log in to reply
I copy your figure and paste it at Paint to edit.
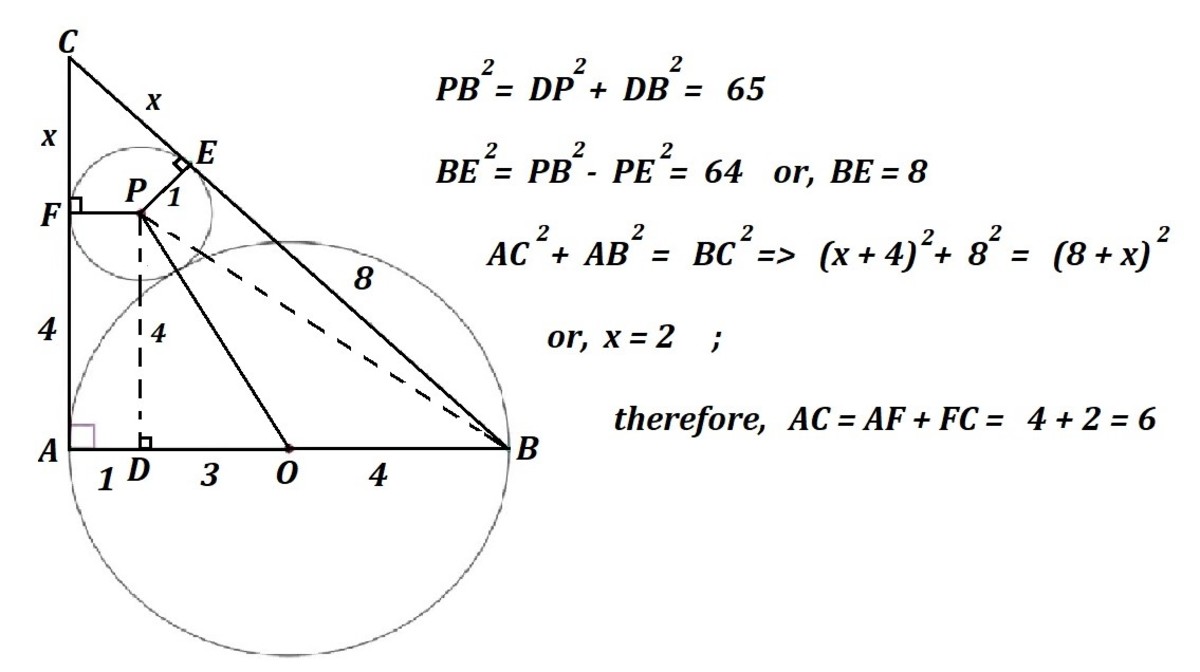
Let O 1 be the center of the circle with radius 1 , O 2 be the center of the circle with radius 4 , then drop a perpendicular line from O 1 to A B , and such that O 1 D is perpendicular to A B . Then we have O 1 D = 4 . And then the area of ∆ A B C is 4 ( ? ) , which then have
4 ( ? ) = 2 ( 1 ) ( ? ) + ( 8 ) ( 4 ) + ? 2 + 6 4 ( 1 ) ? = 6
nice solution!
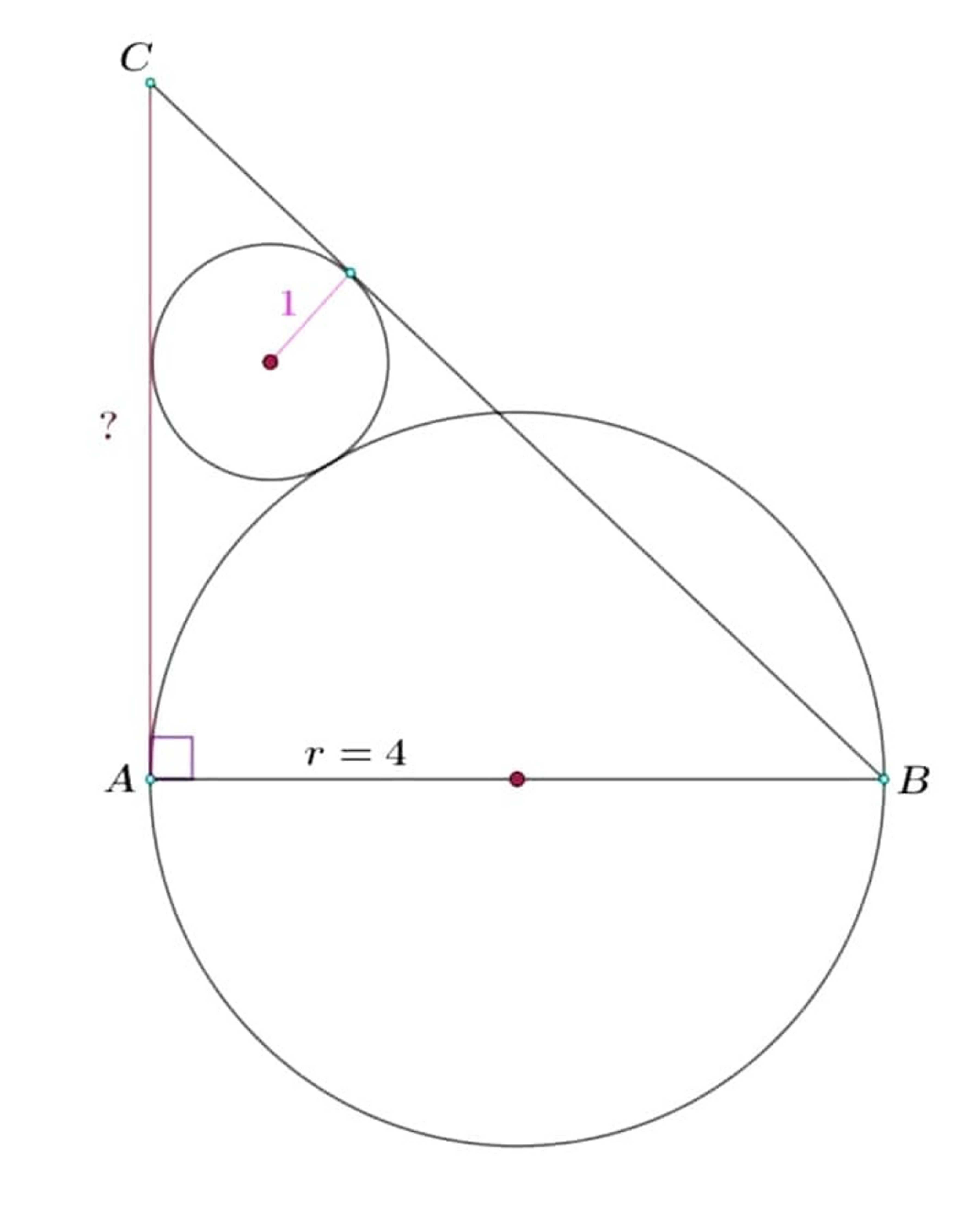
Let the center of circle with radius 1 be O and O D be perpendicular to A C . Let C D = x and ∠ D C O = θ . Then ∠ A C B = 2 θ . It is easy to see that A D = O Q = 4 . The A C = x + 4 . We have:
tan ∠ D C O tan ∠ A C B ⟹ x + 4 8 4 x 2 − 4 3 x 2 − 4 x − 4 ( 3 x + 2 ) ( x − 2 ) ⟹ x = tan θ = C D O D = x 1 = tan ( 2 θ ) = A C A B = x + 4 8 = 1 − x 2 1 x 2 = x 2 − 1 2 x = x 2 + 4 x = 0 = 0 = 2 Since x > 0
Therefore, A C = x + 4 = 6 .