Hidden Roots Part 2
F ( x ) = x − 1 1 + x − 2 1 + x − 3 1 + … + x − 9 9 1 + x − 1 0 0 1
Given the above function F ( x ) and
x 1 , x 2 , … , x n are its roots in some order.
Find the maximum possible value of value
n
+
1
[
x
1
]
−
[
x
2
]
+
[
x
3
]
−
[
x
4
]
+
…
±
[
x
n
]
Details and Assumptions
[ m ] represents greatest integer function of m
Also try Hidden Roots
The answer is 25.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
3 solutions
Discussions for this problem are now closed
Classy but seen somewhere
This was an Amazing problem! @shubhendra singh
Thanks SG.
It is note that F ( x ) = ∑ n = 1 1 0 0 x − n 1 has roots when not all the denominators are positive or negative. Therefore, there is no root for x ≤ 1 and x ≥ 1 0 0 . And there are 9 9 roots such that: ⌊ a n ⌋ = n , where n = 1 , 2 , 3 . . . 9 9 . See the graphs below.
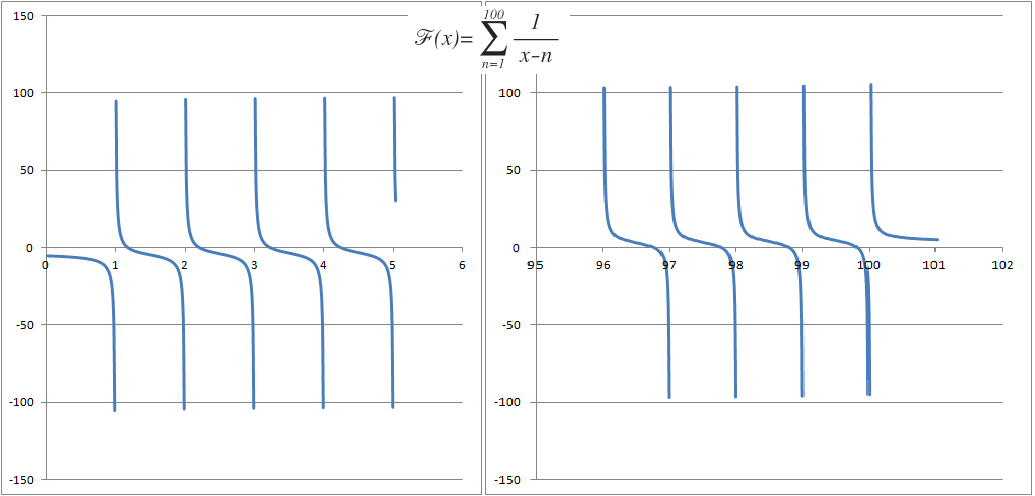
Therefore, the required answer is:
9 9 + 1 9 9 − 1 + 9 8 − 2 + 9 7 − 3 + . . . + 5 1 − 4 9 + 5 0 = 1 0 0 2 5 0 0 = 2 5
Adding 1st & last term, we have (2x-101)/(x-1)(x-100) Similarily 2nd & second last term = (2x-101)/(x-2)(x-99) So, function = (2x-101) [ 1/(x-1)(x-100) + 1/(x-2)(x-99)+.....+1/(x-50)(x-51)] Function has only one root , x = 50.5 GIF(x) = 50 Hence 50/2 = 25 Answer
Consider a polynomial function f ( x ) with roots 1 , 2 , 3 , … . f ( x ) = ( x − 1 ) ( x − 2 ) … ( x − 1 0 0 ) Taking log both sides:- l o g ( f ( x ) ) = i = 1 ∑ 1 0 0 l o g ( x − i ) Differentiating wrt to x :- f ( x ) f ′ ( x ) = i = 0 ∑ 1 0 0 x − i 1 = F ( x ) Question is talking about the roots of F ( x ) which are same as the roots of f ′ ( x ) .
Now, f ( x ) is a polynomial of degree 1 0 0 , so f ′ ( x ) is a polynomial of degree 9 9 . Hence f ′ ( x ) has 9 9 roots.
Also by Rolle's Theorem, Their lies at least 1 root of f ′ ( x ) between any two roots of f ( x ) . So we have 9 9 roots of F ( x ) each lying between two consecutive integers between 1 to 1 0 0 . The values of [ x i ] ′ s are 1 , 2 , 3 , 4 , … 9 9 .
We have to arrange the values so that we get the maximum value of the given expression. The expression can be expressed as:- 9 9 + 1 9 9 − 4 9 + 9 8 − 4 8 + … 5 1 − 1 + 5 0 = 1 0 0 5 0 × 5 0 = 2 5