Hidden Similarity

Geometry Level 1

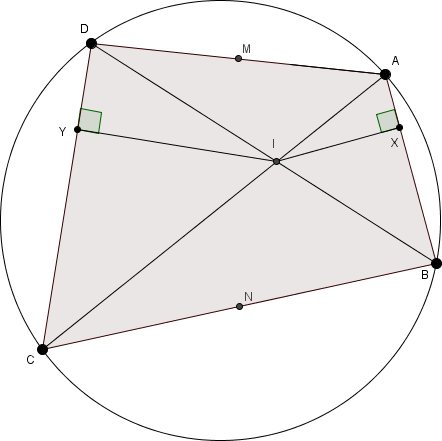
The points $A, B, C$ and $D$ are ordered clockwise on a circle.

$M$ and $N$ are the midpoints of $AD$ and $BC$ , respectively.

$I$ is the intersection of $AC$ and $BD$ .

$X$ and $Y$ , are perpendiculars on $AB$ and $CD$ respectively, which pass through $I$ .

Is $MXNY$ always a kite?

Yes No

2 solutions

Jack Lam
Apr 29, 2016

A bit busy currently, but Spiral Similarity is sufficient to show the central kite is similar to two externally constructed kites on ABCD.

I assumed some cases and based on that I concluded that it is always the same

Syed Baqir - 5 years, 1 month ago

Vishwash Kumar Γξω
Apr 19, 2017

Let $P$ and $Q$ be the midpoints of $CI$ and $BI$ respectively. Join $YP , PN , XQ$ and $QN.$

Clearly, $YP = IP = \frac{1}{2} IC = NQ$ . Similarly, $PN = XQ.$ Some trivial angle chase tells that $\angle YPN = \angle NQX$ => $\triangle YQN \cong \triangle NQX$ => $YN = XN$ . Similarly, one can easily prove it that $MY = MX$ . So, $MXNY$ is always a Kite.

Hidden Similarity

2 solutions

0 pending reports