Hidden Superellipse?
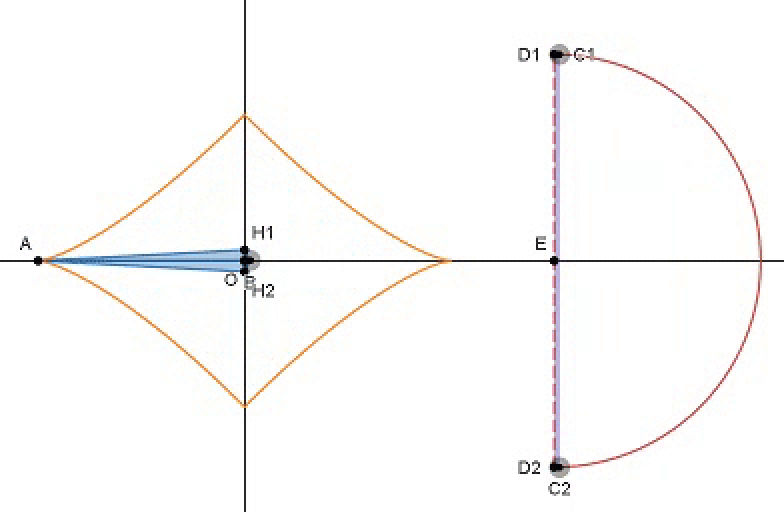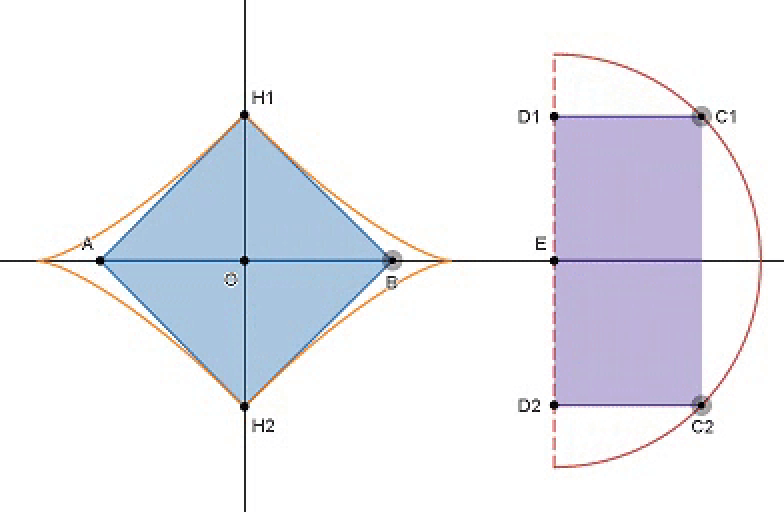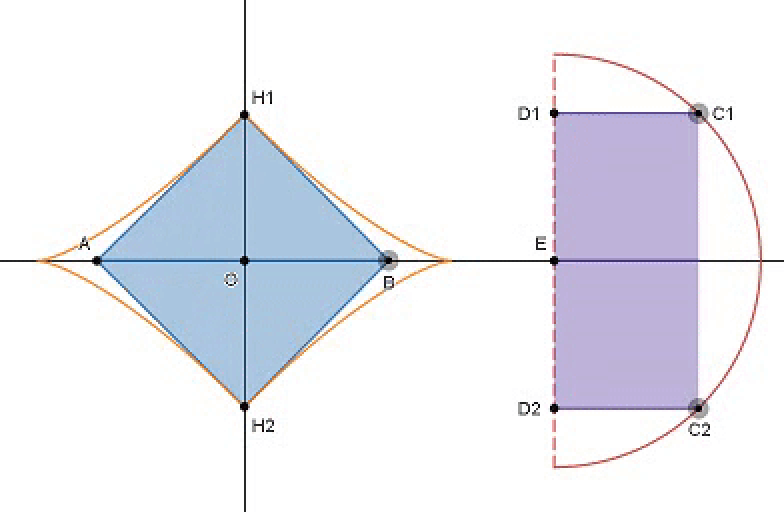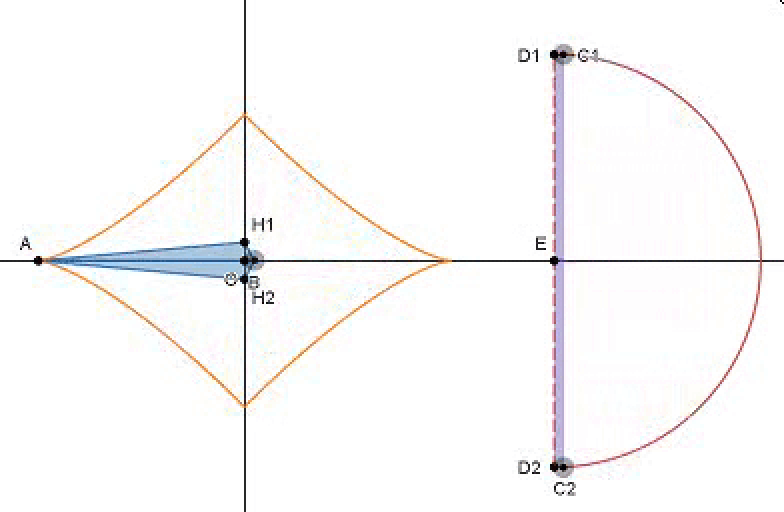
The diagram depicts the orange region bounded by the center of origin and the red semicircle of radius 1 positioned on the right. As shown, both blue and purple symmetric polygons of congruent areas are formed within their respective regions. Throughout the animation, they shape-shift as follows:
- For the blue quadrilateral, the heights and bases of both largest symmetric triangles change.
- For the purple rectangle, both halved rectangles are symmetric about the horizontal axis.
- , whereas
If the area of the orange region can be expressed as where and are nonnegative integers and , input as your answer.
The answer is 11.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
Let E ≡ ( d , 0 ) for some d .
By assuming a paramater t ∈ ( 0 , 2 π ) , the points can be written as:
D 1 ≡ ( d , sin t )
D 2 ≡ ( d , − sin t )
C 1 ≡ ( d + cos t , sin t )
C 2 ≡ ( d − cos t , sin t )
∣ A O ∣ = ∣ D 1 E ∣ = ∣ D 2 E ∣ = sin t ⟹ A ≡ ( − sin t , 0 )
∣ B O ∣ = ∣ D 1 C 1 ∣ = ∣ D 2 C 2 ∣ = cos t ⟹ B ≡ ( cos t , 0 )
As the quadrilateral is symmetric about the x-axis, ∣ H 1 O ∣ = ∣ H 2 O ∣
Therefore, area of the quadrilateral = 2 1 ⋅ ( 2 ⋅ ∣ H 1 O ∣ ⋅ ( sin t + cos t ) ) = ∣ H 1 O ∣ ⋅ ( sin t + cos t )
As the areas of the quadrilateral and rectangle are supposed to be the same:
∣ H 1 O ∣ ⋅ ( sin t + cos t ) = ( cos t ) ( 2 sin t ) ⟹ ∣ H 1 O ∣ = sin t + cos t 2 sin t cos t
This gives us:
H 1 ≡ ( 0 , sin t + cos t 2 sin t cos t )
H 2 ≡ ( 0 , − sin t + cos t 2 sin t cos t )
The equation of the line [segment] joining H 1 and H 2 is given by:
cos t x + 2 sin t cos t y ( sin t + cos t ) = 1 ( x , y > 0 )
⟹ x + 2 y ( 1 + cot t ) − cos t = 0 ( 1 )
The above equation represents a family of lines as t varies from 0 to 2 π .
The curve that is a tangent to the above family of lines is known as the envelope of the family and the method can be found here . Following the given method:
Differentiating with respect to t:
2 y ( − csc 2 t ) + sin t = 0 ⟹ 2 y = sin 3 t
Now, if the above result were to be substitued back in (1) by replacing t in terms of y , it can be seen that it would be quite messy and finding the area would be cumbersome.
Instead, we may substitute y in terms of t and we get:
x = cos t − sin 3 t ( 1 + cot t )
Area is given by: a ∫ b x ( t ) y ′ ( t ) d t
Here, it can be observed that for some values of t , the line segment in the first quadrant does not actually touch the envelope. It is not too tough to see that for t ∈ ( 0 , 4 π ) , the quadrilateral is more on the right and is touching the envelope. Therefore, the limits of the integral are 0 and 4 π .
∴ A = ∫ 0 4 π ( x ( t ) ) ( y ′ ( t ) ) d t
⟹ A = ∫ 0 4 π ( cos t − sin 3 t ( 1 + cot t ) ) ( 6 sin 2 t cos t ) d t
⟹ A = 6 ∫ 0 4 π ( sin 2 t cos 2 t − sin 5 t cos t − sin 4 t cos 2 t ) d t
⟹ A = 6 ∫ 0 4 π ( sin 2 t cos 4 t − sin 5 t cos t ) d t
The above integral isn't too tough to solve manually with appropriate substitutions. Therefore, skipping the calculations, we get that:
A = 3 2 3 π
As the figure is given to be symmetric about the x-axis, the area in the fourth quadrant is also A . I also claim that the the figure is symmetric about the y-axis for which I shall not provide the justification, convince yourself. In the case that you aren't able to convince yourself, you may follow the same procedure to explicitly get the area on the left side.
Finally, total area = 4 A = 8 3 π ⟹ A = 3 , B = 8 ⟹ A + B = 3 + 8 = 1 1