Hideous Arrangement of Circles
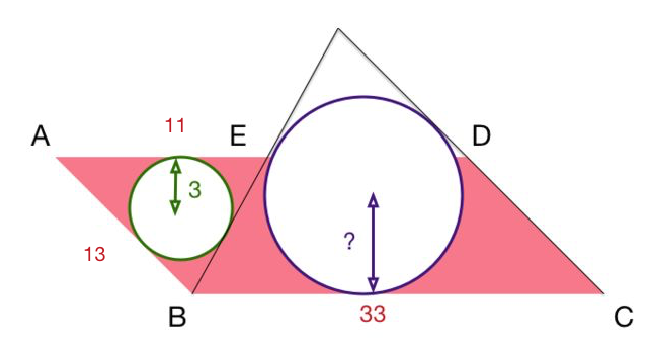
A B C D is a parallelogram where A B = 1 3 and B C = 3 3 . A point E is taken on A D such that A E = 1 1 . If the inradius of △ A B E is of length 3 , find the radius of the circle touching E B , D C and B C .
The answer is 9.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
Nice and easy!
I saw that an image was added to my problem very recently. I have removed the image because I think it gives away the construction. I appreciate whoever put the image. I know it took you a lot of effort. My apologies to you.
Update: I realised I could use the image in the solution so that is what I did. Thanks a lot, buddy : ) !
Log in to reply
Hi Milind,
As we are featuring the problem, we would like to keep the image so that others can easily understand what you are describing. I have added the image back (and udpated the lengths).
How AEB is similar to DEX
Log in to reply
∠ A E B = ∠ D E X because they are vertically opposite angles. Also A B is parallel to C D . Hence, ∠ B A E = ∠ E D X as they are alternate interior angles. So, △ A E B is similar to △ D E X by the Angle-Angle Similarity criterion.
In your first line, I think you mean "Extend B E ", not "Extend A E ".
Sorry if this is too trivial, why did you find DX?
Why do you calculate DX and you don't use it after? I think you don't need to prove triangle AEB is similar to triangle DEX. We can prove directly triangle CBX is similar to triangle AEB. Angle DAB is equal to angle DCB (because ABCD is a parallelogram), and angle AEB is equal to angle EBC.
Also, proving the ratio between inradii equals to the ratio between two sides is easy, by using S=pr (p is half the perimeter, r is the inradius).
This problem is not so hard. It must be level 3 or 4 instead.
Log in to reply
Oh ya! I wonder why I went on the wild goose chase. I have trimmed the solution. Thanks!
I too was surprised when my problem hit level 5. (It started out as a level 3 problem). I expect it to level down anytime soon because the figure that has been added eliminates the need to "think up" the construtction.
I used comoonendo-dividendo to prove it.
Log in to reply
That's great! You should submit your solution too :)
This is same as that of Milind Prabhu. I am presenting as I saw it.
Since the sides of the truncated triangle EBCD were same or parallel, they seemed to be similar. So I extended BE and CD to meet at X.
Δ
X
C
B
Δ
B
A
E
,
the ratio of sides opposite to BXC and EBA is 3. So required inradius=3*3=9. What I was wondering is, should the circle be with in BCDE?
Using Heron's formula and the area formula for a triangle B E works out to be of length 2 0 . Using the law of cosines and a calculator ∠ B A E = 1 1 2 . 6 2 ∘ . Therefore ∠ A B C = 6 7 . 3 8 ∘ . Drop a perpendicular from A to B C and let its foot be Y . The height A Y of the parallelogram turns out to be 1 2 . This is less than the diameter of the circle tangent to B E , B C and C D . So, I think the circle will not be within B C D E .
@Niranjan Khanderia Please do tell me if there is a mistake. Thanks a lot for pointing that out! I have removed the figure because I think it will be really misleading.
Log in to reply
You are correct. But it can be seen much easily. I also saw it just now. Since AB=13, height of the parallelogram can not be more than 13, but the diameter is 18. So the incircle will not be within
BCDE.
I think all most all put BCDE,AB=13 ... in Latex. I do not unless, I want Latex to perform maths with say AB, which I do no not do in my solution.
Again when we have only one letter there is no need to put it with in {..}.....Say 28^2 , A_4, \dfrac12(meaning 1/2). No harm if {..} is used.
Take care:- \dfrac m n,( meaning m/n ) m and n are letters, so keep space, otherwise \dfrac mn, or \dfracm n, carry no meaning to Latex, first it takes mn as single variable, second there is no word like dfracm in Latex.
Construction: Extend B E to meet D C extended at X say.
∠ A E B = ∠ X B C and ∠ E A B = ∠ D C B .Hence, △ C B X is similar to △ A E B . The inradii of similar triangles are in the same ratio as their sides(Try to prove this!). The length of the inradius of △ C B X is, therefore, 3 times the length of the inradius of △ A E B .
Thus, the length of the required inradius is 9 .