Hiding behind a goldfish
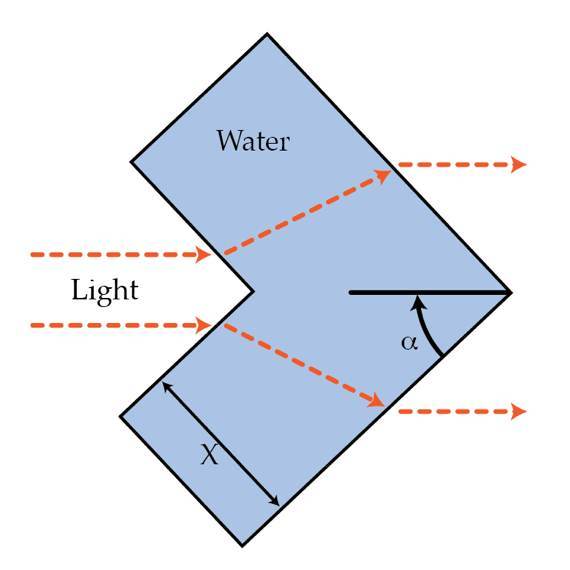
Things can be made invisible in one direction using a combination of lenses and mirrors which would bend the light around them. One way to hide a certain area is to build a big aquarium with water as shown in the picture that will bend the light.
What should be the width X of the aquarium in m so that we can hide 1 m of space? 1 m of space means the distance between the outgoing light rays in the figure is 1 m.
Details and assumptions
- The refractive index of water is 1 . 3 3 .
- The prism angle α of the aquarium is 3 0 ∘ .
The answer is 1.144.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
Initially when the water enters the aquarium, it changes its direction: sin ( 9 0 ∘ − α ) = n sin ( β ) , where β is the angle the light makes in the aquarium with the normal.
When the light goes out of the aquarium, the exiting angle is the same as the entering angle into the aquarium since the relative refractive index of the boundaries is the same. The length L traveled by the light ray in the aquarium is L = X / c o s β . The vertical displacement of the light ray (equal to d / 2 ) is d / 2 = L s i n γ where γ = 9 0 − α − β . Using d = 1 yields \X=1.144).
After a geometrical consideration of the system, we can derive that the light ray shifts for d = l cos ( α ) ( 1 − n sin ( α ) ) , where l is the width of aquarium. Since we need to hide 2 d = 1 m , we can calculate l to be l = 2 . 8 6 6 5 m .
The incoming rays form an angle of (90-α) = 60 degrees with the normal, which is the angle of incidence.
Using Snell's law, we can find the angle of refraction (r): 1.33 = sin 60 / sin r hence r = 40.63 degrees.
Now, the angle of the refracted ray with the horizontal is [(90-r) - (90-i)]= (i-r) = 19.37 degrees.
Let the length of the refracted ray be L. Then L sin(i-r) is also the vertical shift = 0.5 m L cos(r) = X
Solving yield X = 1.14 m