High Bounce

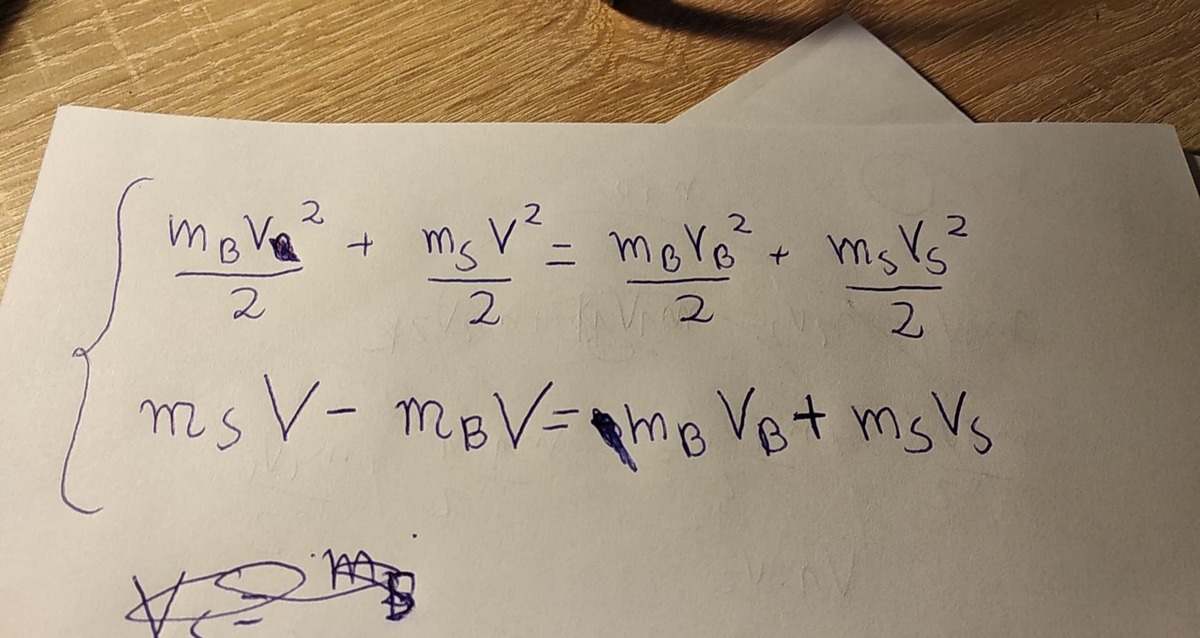
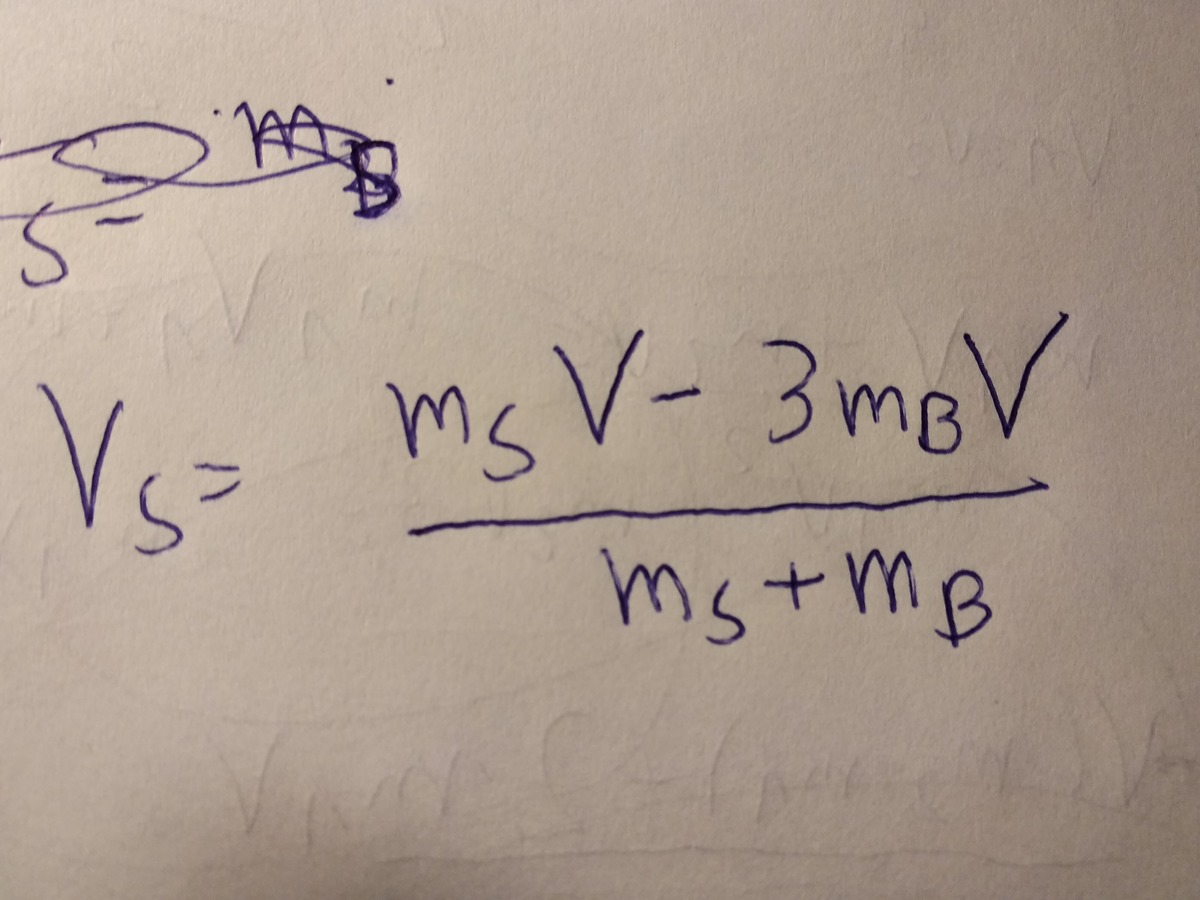
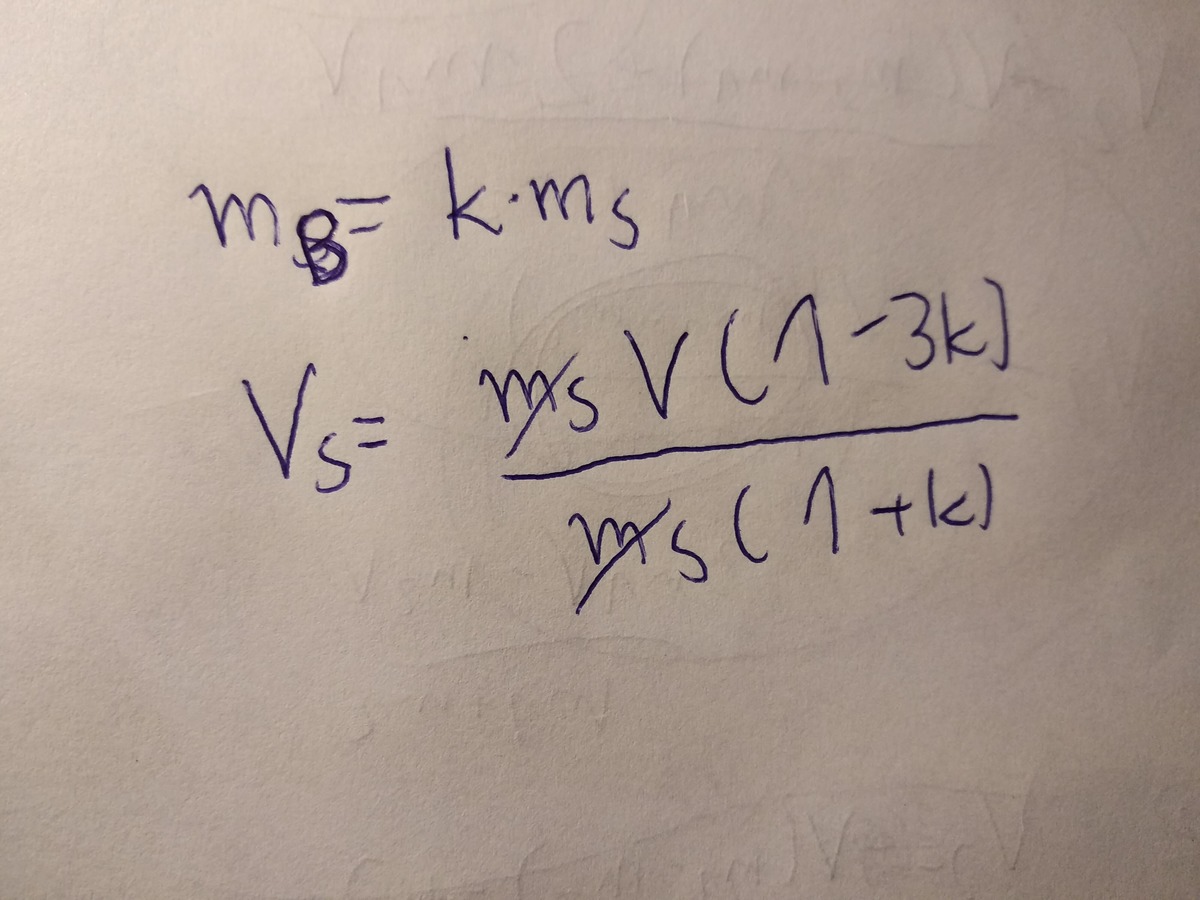
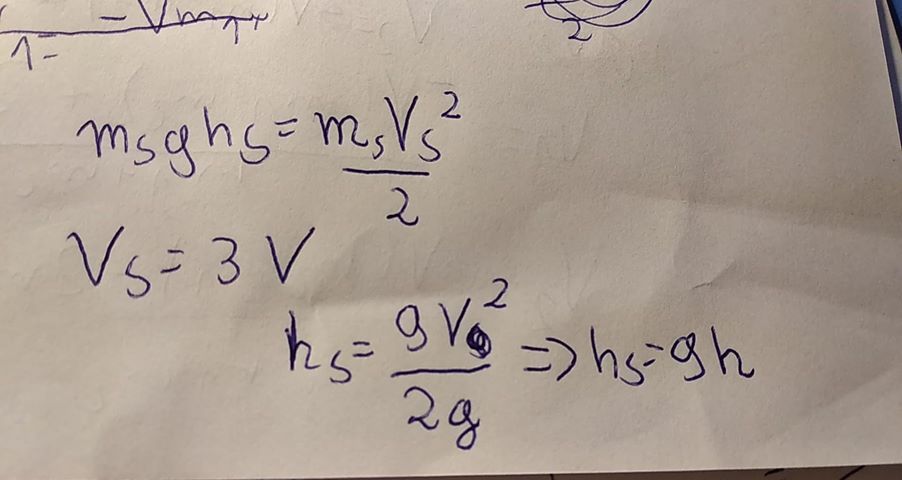
The formula for the height difference of lighter ball is:

$\Delta h = \frac{8M(M-m)}{(M+m)^{2}}$

Maximum of this expression is equal to $\boxed{8}.$

Hint : Treat the collision from center of mass frame, it will save you some time.

Derivation :

Denote $v_{o}$ to be the speed of the falling balls relative to the ground at the moment when the heavier one hits the ground (they will both gain the same speed because they travel the same distance in the gravitational field, acceleration of which we are assuming is constant), $M$ to be the mass of the heavier ball and $m$ to be the mass of the lighter ball. Assuming elastic collision with the ground, heavier ball starts moving up with the equal velocity - $v_{o}$ - and collides with the lighter ball with velocity $v_{o}$ in the downward direction. Further on, denote $v_{CoM}$ to be the speed of centar of mass frame (CoM frame) relative to the ground, $v'_{h}$ and $v'_{l}$ to be the speed of the heavier and lighter ball relative to CoM frame, and $v_{h}$ and $v_{l}$ the speed of the heavier and lighter ball relative to the ground, respectively. Now, let us examine the collision between two balls in the CoM frame (positive direction is upward direction):

Momentum of two balls

$v_{CoM} = \frac{M}{M+m}v_{o} - \frac{m}{M+m}v_{o} = v_{o}\frac{M-m}{M+m}$

$\begin{aligned} v'_{h} &= v_{o} - v_{CoM} = v_{o}\frac{2m}{M+m} \\ v'_{l} &= -v_{o} - v_{CoM} = -v_{o}\frac{2M}{M+m} \end{aligned}$

These are the speeds before collision, but, as you will see, it won't be hard to find the speeds after collision. Since we are making measurements in CoM frame, balls have equal momentum, so they apply the same force on each other, and thus exit the collision with equal speeds but in opposite directions. We have:

$\begin{aligned} v_{h} &= -v'_{h} + v_{CoM} = v_{o}\frac{M-3m}{M+m} \\ v_{l} &= -v'_{l} + v_{CoM} = v_{o}\frac{3M-m}{M+m} \end{aligned}$

Finally, we have:

$\begin{aligned} 2g(h_{l} + \Delta h_{l})&= v_{l}^{2} \\ 2g(1 + \Delta h_{l})&= v_{o}^{2}\left ( \frac{3M-m}{M+m} \right )^{2} \quad \quad {\color{#0C6AC7} v_{o}^{2} = 2g} \\ 1+\Delta h_{l} &= \left ( 1 + 2\frac{M-m}{M+m} \right )^{2} \\ \Delta h_{l} &= 4\frac{M-m}{M+m} + 4\frac{(M-m)^{2}}{(M+m)^{2}} \\ \Delta h_{l} &= \frac{4M^{2} - 4m_{2}^{2} + 4M^{2} - 8Mm + 4m^{2}}{(M+m)^{2}} \\ \Delta h_{l} &= \frac{8M(M-m)}{(M+m)^{2}}\end{aligned}$

Define new variable $\gamma = \frac{m}{M}$ . We expect to achieve a maximum height when this ratio is close to zero, which can be proven by calculus:

$\displaystyle{\lim_{\gamma \to 0} \frac{8(1-\gamma)}{(1+\gamma)^{2}} = 8}$

Check out this chapter in Brilliant's Classical Mechanics course for deeper understanding of CoM frame and it's advantages.

First of all we can notice that just before the collision, after the bigger ball will hit the ground value of velocities of both balls will be the same (vectors will have opposite directions) and we know this from conservation of energy and the fact that all collisions (including this one when bigger ball hit the ground) are perfectly ellastic. We can easily determine that the value of this velocity will be V= $\sqrt{2gh}$ where h is one meter. Now we know that two balls will hit each other and collision as we said will be perfectly ellastic, so energy and momentum of two balls is constant. Knowing this we get: ms- mass of smaller ball, mb- mass of bigger ball, V- velocity before collision, Vs- velocity of smaller ball after collision, Vb-Velocity of bigger ball after collision.

I put minus in one place because i assumed that "plus" direction of velocity is down (in the same direction as vector of gravity force to say it more precisely).

We are interested in velocity of smaller ball so we resolve this system of equations and get: As we can see this velocity depends on masses of balls. We do not know any of them, but we can elliminate one of them defining ratio of mass of bigger ball to smaller by k, where k is real number and k>1. Thus we have: Now we have to find the biggest possible value of Vs, but differentiating won't help us. The thing that will help is looking at graph of function $\frac{1-3k}{1+k}$ : The values for k>1 are obviously under zero, because direction of the velocity after collision is up, which is "minus direction". As we can see the bigger k the bigger absolute value of velocity is, hence we realise that the biggest value of velocity will be reached when k is approaching infinity. Taking limit from the Vs when k goes to infinity will show us that the biggest value of Vs is triple of value of V (velocity before collision). Using last time conservation of energy and the fact that V= $\sqrt{2gh}$ we can determine that: Where hs is height which the smaller ball reaches after the collision. We can easily see that difference between this two heights is 8m, because h=1m.

The smaller ball which is incoming with a velocity acquired in the fall, hits the bigger ball returning with the same velocity after hitting the ground. Considering the conservation of energy and momentum in the elastic collision of the big and smaller ball, the smaller ball will return with almost thrice the velocity and thereby gain almost nine times the fall height.