Highest Points
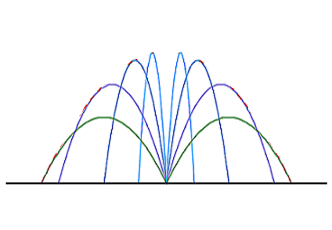
Suppose at initial height 0, one casts a projectile into the air with constant initial velocity v but different elevation angles in the same vertical plane. The area of the region that highest points enclose is
A = α g 2 v 4 .
What is the value of positive number α ?
Neglect air resistance.
The answer is 0.392699.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
How do we eliminate θ from X and Y equations ?
Log in to reply
Note that sin 2 θ = 2 1 − cos 2 θ and sin 2 2 θ + cos 2 2 θ = 1 .
I got X and Y as Brian did (those formulas can be found in introductory physics texts as well), and then let A = ∫ θ = 0 π X d Y = 4 g 2 v 4 ∫ θ = 0 π sin 2 ( 2 θ ) d θ = 8 g 2 v 4 π The answer is α = 8 π ≈ 0 . 3 9 2 7
At any time t , the projectile's horizontal and vertical displacement are
x y = v t cos θ , = v t sin θ − 2 1 g t 2 .
The increase in height will last until v y = 0 , that is, 0 = v sin θ − g t . Thus, time to reach the maximum height is given by
t = g v sin θ .
Substituting this value into the equations above, we get coordinates of highest point
X Y = 2 g v 2 sin 2 θ , = 2 g v 2 sin 2 θ .
If θ is eliminated between these two equtions, the following eqution is obtained
( 2 g v 2 ) 2 X 2 + ( 4 g v 2 ) 2 ( Y − 4 g v 2 ) 2 = 1 .
Therefore, the set of all highest points is a ellipse centered at ( 0 , 4 g v 2 ) with semi-major and semi-minor axes 2 g v 2 and 4 g v 2 respectively. Its area is
A = π ( 2 g v 2 ) ( 4 g v 2 ) = ( 8 π ) ( g 2 v 4 ) ,
making the answer 8 π .