Highly Wedged Constraint Motion!!

Classical Mechanics Level 3

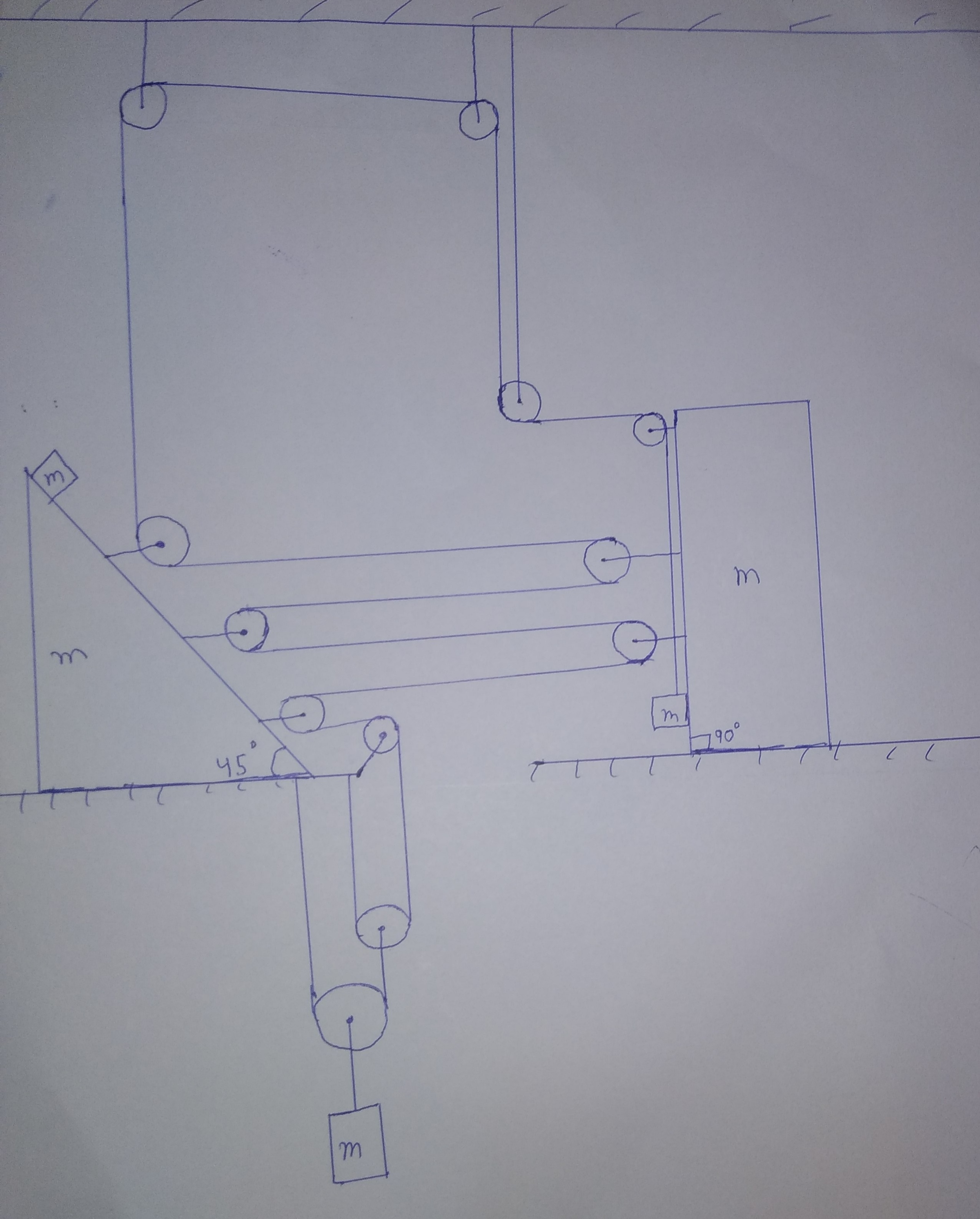
Find $\color{#20A900}{acceleration}$ of $\color{#20A900}{\text{Lowest Hanging Block}}$ $(\text{ in } m/s^2)$ in above system. If your answer can be expressed of form $\color{#20A900}{\frac{a}{b}} \color{#333333}{\text{ where } a, b \in I^+ \text{ and } gcd(a, b) = 1}$ , Enter your answer as $\color{#20A900}{a + b}$ .

Details and Assumptions

All surfaces are $\color{#20A900}{smooth}$
All $\color{#20A900}{strings}$ and $\color{#20A900}{pulleys}$ are $\color{#D61F06}{ideal}$
All $\color{#20A900}{Wedges}$ and $\color{#20A900}{blocks}$ are $\color{#20A900}{free}$ to move.
Take acceleration due to gravity $\color{#20A900}{g = 10m/s^2}$
Strings are $\color{#D61F06}{not}$ intermingled.

All of my problems are original

Difficulty: $\dagger \dagger \dagger \dagger \color{grey}{\dagger}$

The answer is 897.

1 solution

Aryan Sanghi
Jul 6, 2020

Here is a F.B.D. for all bodies considering only Forces responsible for motion.

We get equations

$Nsin\theta - 5T = mA_1$

$mgsin\theta = ma_x$

$mgcos\theta - N = ma_y = mA_1sin\theta$

$N' = mA_3$

$5T - N' = mA_3$

$T - mg = mA_4$

$4T - mg = mA_2$

Using Tension trick(Just Work-Energy theorem) to find constraint relation

$\sum T.A = 0$

$-5T × A_1 + 4T×A_2 + 5T × A_3 + T×A_4 = 0$

$\boxed{-5A_1 + 4A_2 + 5A_3 + A_4 = 0}$

Solving all equations, we get

$T = \frac{40mg}{227}$

$A_2 = \frac{67g}{227} = \frac{670}{227}$

$\color{#3D99F6}{\boxed{a + b = 897}}$

A good problem 👍

Kundan Rathi - 11 months, 1 week ago

Thanku. :)

Aryan Sanghi - 11 months, 1 week ago

Highly Wedged Constraint Motion!!

Details and Assumptions

Difficulty: † † † † † \dagger \dagger \dagger \dagger \color{grey}{\dagger} † † † † †

The answer is 897.

1 solution

0 pending reports

Difficulty: $\dagger \dagger \dagger \dagger \color{grey}{\dagger}$