Hinged Rod!

A lengthy approach, but different from that of energy.

$\sum { { \tau }_{ ext } } =I\alpha \\ I\alpha =mg(\cos { \theta } )\frac { l }{ 2 } \qquad [\because \quad It\quad (mg(\cos { \theta } ))\quad is\quad the\quad only\quad component\quad of\quad gravitational\quad force\quad that\quad causes\quad rotation\quad in\quad the\quad rod]\\ \alpha =\frac { mg }{ I } (\cos { \theta } )\frac { l }{ 2 } \\ \alpha =\frac { mg }{ \frac { m{ l }^{ 2 } }{ 3 } } (\cos { \theta } )\frac { l }{ 2 } \quad \qquad [\because \quad rotational\quad inertia\quad (I)\quad for\quad the\quad rod,\quad with\quad rotational\quad axis\quad through\quad end,\quad is\quad \frac { m{ l }^{ 2 } }{ 3 } ]\\ \\ Simplifying\quad we\quad get:\\ \\ \alpha =\frac { 3g }{ 2l } (\cos { \theta } )\qquad \qquad \qquad \qquad \qquad \qquad \qquad (1)\\ \\ \because \quad the\quad angular\quad acceleration\quad of\quad the\quad rod\quad varies\quad with\quad its\quad angular\quad position\quad (\theta ),\\ rotational\quad kinematic\quad expressions\quad are\quad of\quad no\quad use.\\ So,\\ \\ \alpha =\frac { d\omega }{ dt } =\frac { d\omega }{ d\theta } .\frac { d\theta }{ dt } =\frac { d\omega }{ d\theta } .\omega \qquad \qquad [Using\quad chain\quad rule]\\ \alpha .d\theta \quad =\quad \omega .d\omega \\ \int _{ { \theta }_{ i } }^{ { \theta }_{ f } }{ \frac { 3g }{ 2L } (\cos { \theta } )d\theta } =\int _{ { \omega }_{ i } }^{ { \omega }_{ f } }{ \omega \quad d\omega } \\ \\ Solving\quad the\quad integral\quad we'll\quad get:\\ \\ { \omega }_{ f }=\sqrt { { { \omega }_{ i }^{ 2 } }+\frac { 3g }{ l } (\sin { ({ \theta }_{ f }) } -\sin { { (\theta }_{ i }) } ) } \qquad \qquad (2)\\ \\ Initial\quad angular\quad position,\quad { \theta }_{ i }=0\quad from\quad X-axis\quad and\quad final\quad angular\quad position,\quad { \theta }_{ f }=\frac { \pi }{ 2 } \\ Initial\quad angular\quad speed,\quad { \omega }_{ i }=0\quad and\quad final\quad angular\quad speed,\quad { \omega }_{ f }\quad is\quad required.\\ Substituting\quad these\quad in\quad (2)\quad we\quad get:\\ \\ { \omega }_{ f }=\sqrt { \frac { 3g }{ l } } \qquad \qquad \qquad \qquad \qquad \qquad \qquad (3)\\ \\ We\quad know\quad v=r\omega ,\\ \omega ={ \omega }_{ f }\quad and\quad r=l\quad (\because \quad velocity\quad at\quad the\quad end\quad of\quad the\quad rod\quad is\quad asked)\\ \\ v=l\sqrt { \frac { 3g }{ l } } =\sqrt { { l }^{ 2 }\frac { 3g }{ l } } =\sqrt { 3gl } \\ \therefore \quad \boxed{v=\sqrt { 3gl } }$

As the mass is concentrated at the center of the rod.....therefore.....

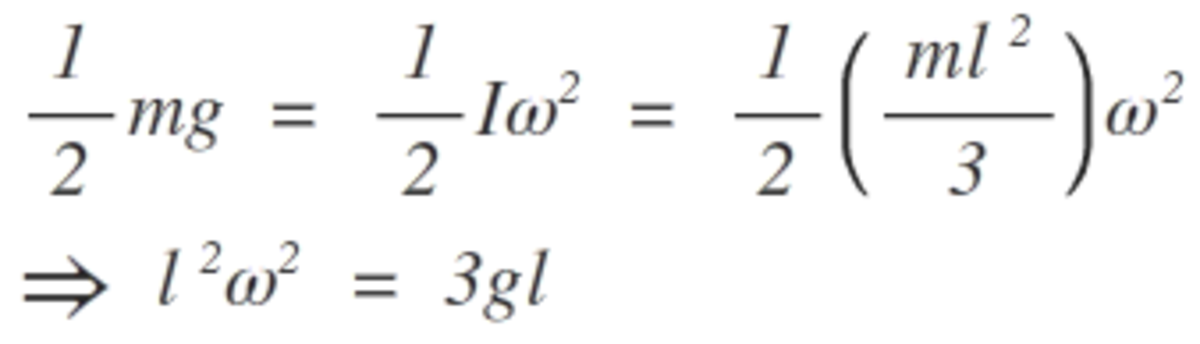
Thus , the velocity at the other end of the rod is ...........

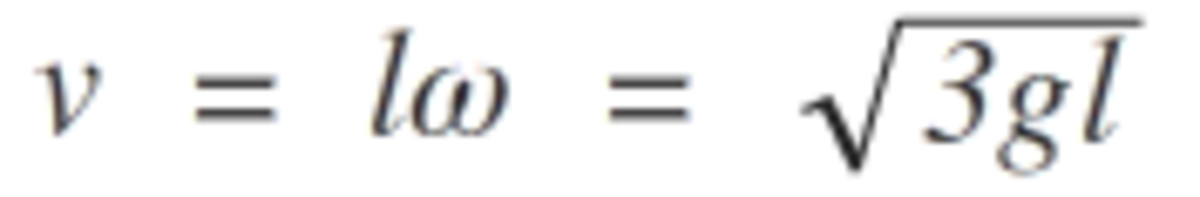
This is my solution.....if anyone finds any error please feel free to correct me !!!!!

Enjoy And Learn !!!!!