Hoci Foci Loci
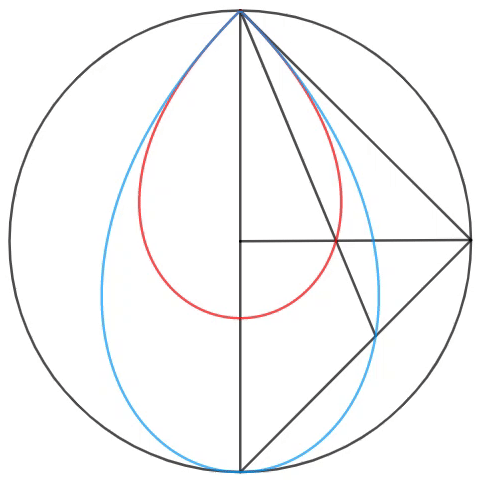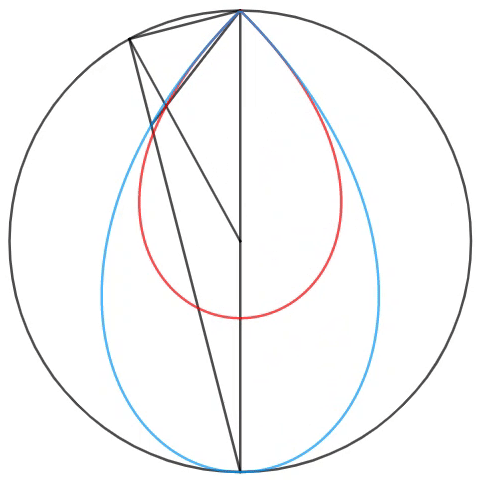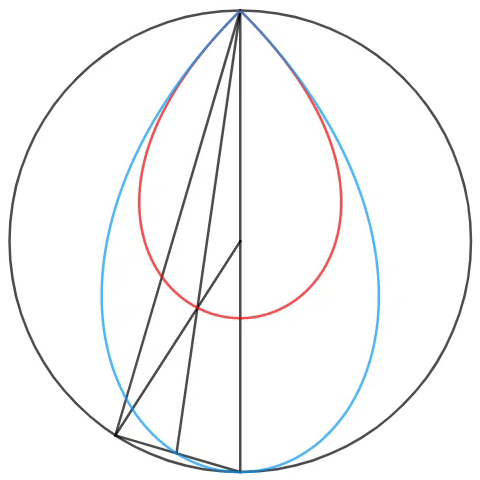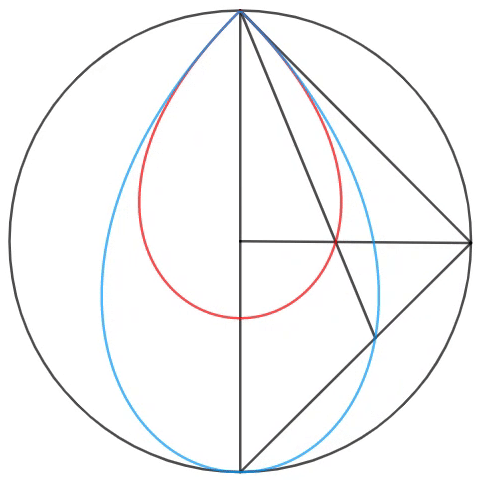
In the circle, a point is selected along the circumference, forming three triangles - two isosceles triangles and one right triangle (the largest) - each with fixed endpoints and fixed centers on the diameter. As shown above, the angle bisector, intersecting the top point, is formed, so that when the point is rotated counterclockwise, two loci are formed.
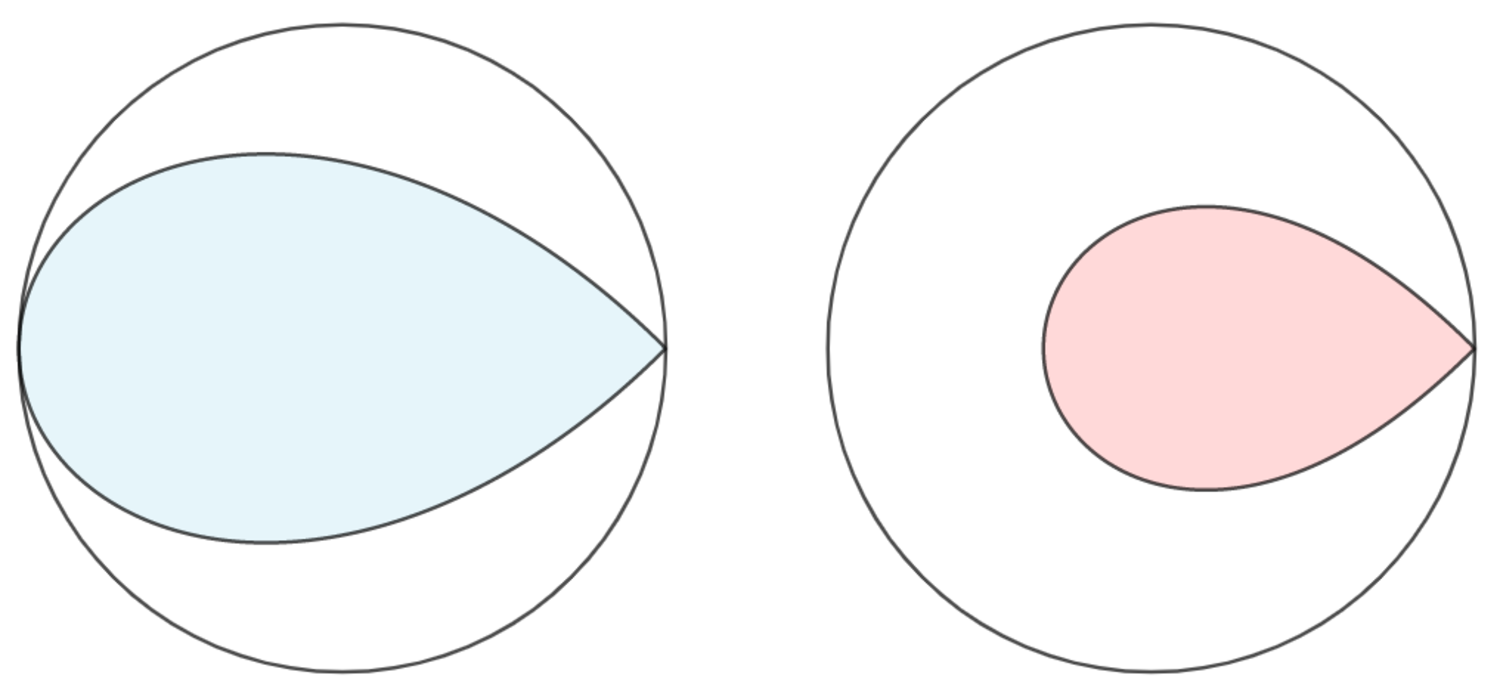
If the ratio of the red area to the blue area is R , input ⌊ 1 0 6 R ⌋ as your answer.
The answer is 481377.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
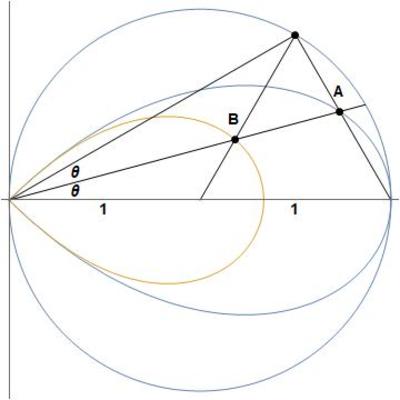 Let the circle have radius
2
. Simple angle-chasing and trigonometry tell us that
r
1
(
θ
)
r
2
(
θ
)
=
O
A
=
cos
θ
2
cos
2
θ
=
O
B
=
sin
3
θ
sin
4
θ
for
∣
θ
∣
≤
4
1
π
. Thus the blue area is
2
1
∫
−
4
1
π
4
1
π
r
1
(
θ
)
2
d
θ
=
8
−
2
π
while the red area is
2
1
∫
−
4
1
π
4
1
π
r
2
(
θ
)
2
d
θ
=
3
4
−
9
4
3
tanh
−
1
3
1
which makes the ratio of areas
R
=
0
.
4
8
1
3
7
7
5
2
1
9
.
.
.
and hence
⌊
1
0
6
R
⌋
=
4
8
1
3
7
7
.
Let the circle have radius
2
. Simple angle-chasing and trigonometry tell us that
r
1
(
θ
)
r
2
(
θ
)
=
O
A
=
cos
θ
2
cos
2
θ
=
O
B
=
sin
3
θ
sin
4
θ
for
∣
θ
∣
≤
4
1
π
. Thus the blue area is
2
1
∫
−
4
1
π
4
1
π
r
1
(
θ
)
2
d
θ
=
8
−
2
π
while the red area is
2
1
∫
−
4
1
π
4
1
π
r
2
(
θ
)
2
d
θ
=
3
4
−
9
4
3
tanh
−
1
3
1
which makes the ratio of areas
R
=
0
.
4
8
1
3
7
7
5
2
1
9
.
.
.
and hence
⌊
1
0
6
R
⌋
=
4
8
1
3
7
7
.
Let the circle be a unit circle with an equation of x 2 + y 2 = 1 , and label the diagram as follows:
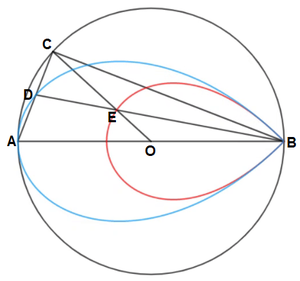
Let the x -coordinate of C be k . Since it is on the circle x 2 + y 2 = 1 , it has a y -coordinate of 1 − k 2 , so its coordinates are C ( k , 1 − k 2 ) .
Then C A has an equation of y = k + 1 1 − k 2 ( x + 1 ) , C O has an equation of y = k 1 − k 2 x , and C B has an equation of y = k − 1 1 − k 2 ( x − 1 ) .
Since B D is the angle bisector of ∠ C B A , by the half angle formula tan ∠ C B A = k − 1 1 − k 2 = 1 − tan 2 ∠ D B A 2 tan ∠ D B A , which rearranges to tan ∠ D B A = k + 1 1 − k 2 − 2 1 + k .
Then D B has an equation of y = k + 1 1 − k 2 − 2 1 + k ( x − 1 ) .
Combining y = k + 1 1 − k 2 − 2 1 + k ( x − 1 ) and y = k + 1 1 − k 2 ( x + 1 ) and eliminating k gives y = ± x − 3 − x 3 + x 2 + x − 1 , the equation of the blue curve, which contains an area of 2 ∫ − 1 1 x − 3 − x 3 + x 2 + x − 1 d x = 8 − 2 π .
Combining y = k + 1 1 − k 2 − 2 1 + k ( x − 1 ) and y = k 1 − k 2 x and eliminating k gives y = ± ( x − 1 ) ( x − 3 ) − 2 ( x − 1 ) 2 ( x 2 − 2 x + 2 ) , the equation of the red curve, which contains an area of 2 ∫ − 3 1 1 ( x − 1 ) ( x − 3 ) − 2 ( x − 1 ) 2 ( x 2 − 2 x + 2 ) d x ≈ 0 . 8 2 6 4 3 6 0 0 2 5 .
The ratio of the red area to the blue area is then R ≈ 8 − 2 π 0 . 8 2 6 4 3 6 0 0 2 5 ≈ 0 . 4 8 1 3 7 7 5 , so ⌊ 1 0 6 R ⌋ = 4 8 1 3 7 7 .