Hocus Pocus Locus

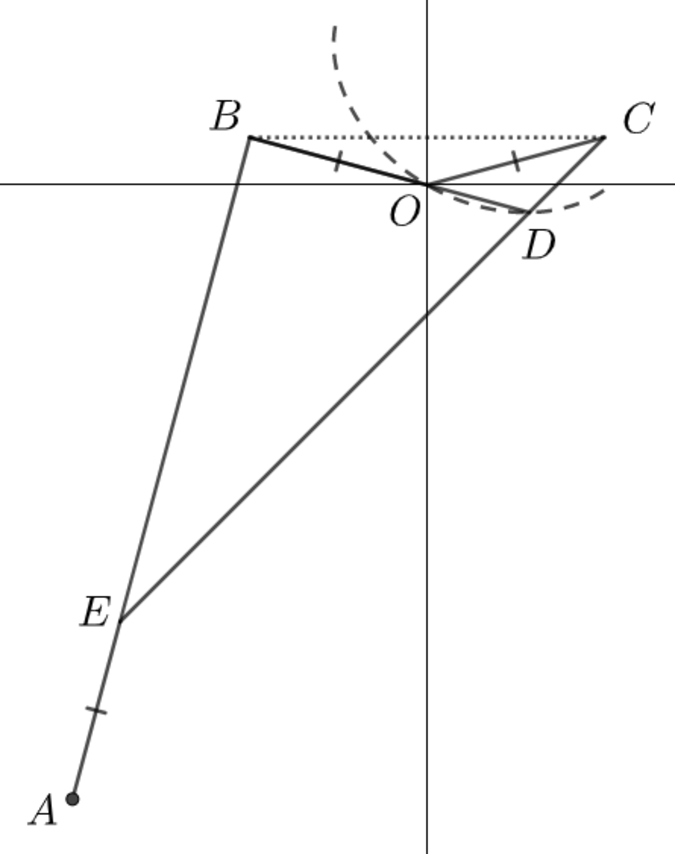
In the rectangular plane, let $A, B, C, D, E$ be points, such that

• $\overline{BC}$ is parallel to the horizontal axis;
• Point $D$ is positioned along the locus;
• $|\overline{AB}| = |\overline{CE}|$ ;
• $|\overline{AE}| = |\overline{BO}| = |\overline{CO}| = 1$ , where point $O$ is the intersection point of two axes;
• $\angle AEC = \angle BOC$

As shown on the right, for $\angle BCO = 15^{\circ}$ , $\overline{BD}$ overlaps $\overline{BO}$ . The following are all possible arrangements, involving $0^{\circ} \leq \theta < 30^{\circ}$ and $30^{\circ} \leq \theta < 60^{\circ}$ respectively, where $\theta$ is one of the acute angles of $\bigtriangleup BOC$ .

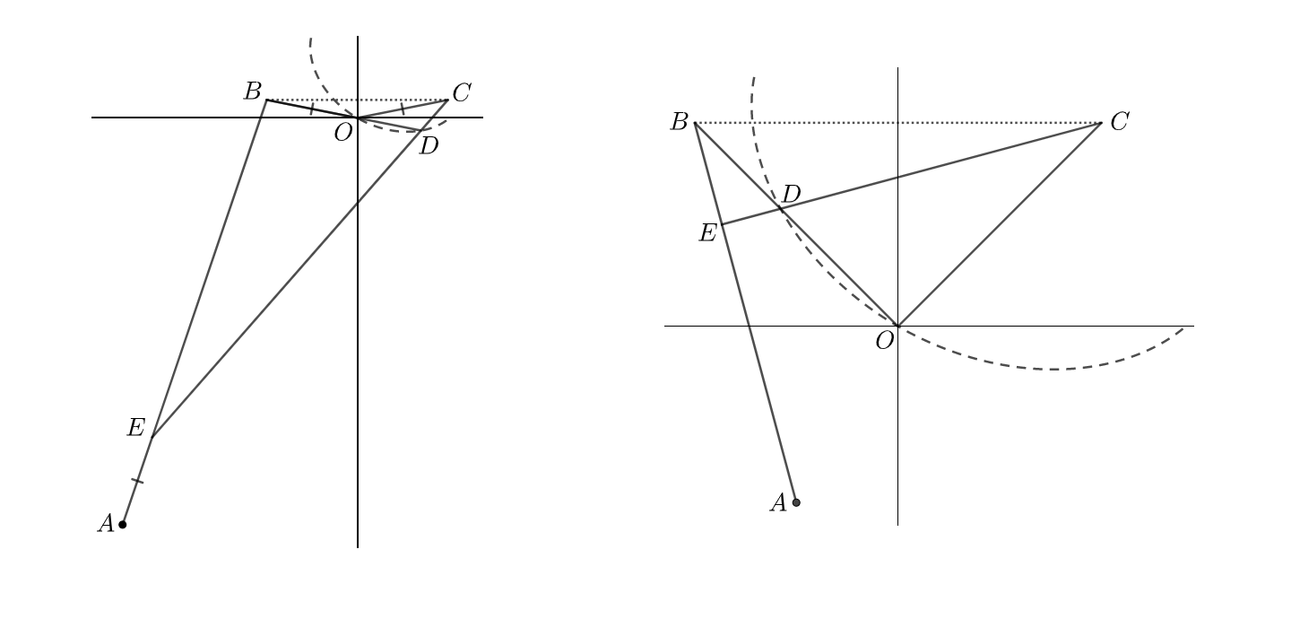
If the arc length of the locus bounded by $0^{\circ} \leq \theta < 60^{\circ}$ is $A$ , input $\lfloor 10^5 A\rfloor$ as your answer.

Bonus. Find the exact value of $A$ .