Hold on, Indy!
A standard action movie scene is the following: the hero or heroine is on a bridge when the most devious evil bad guys cut the supports on one side of the bridge, leaving the hero/heroine to cling desperately to the bridge as it slowly swings down. Then there's the camera shot over the side of the cliff as we wait to see if the hero or heroine actually held on to the bridge and is now climbing back up.
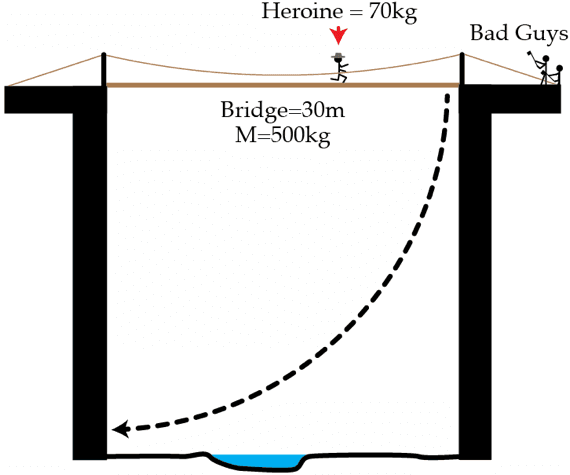
Our 7 0 kg heroine is two-thirds of the way across a horizontal 3 0 m long bridge over a canyon with perfectly vertical walls. The bad guys then cut the supports of the bridge (she is closer to where the supports are cut than the other side). The bridge, which can be modeled as a rod of mass 5 0 0 kg and uniform density, then begins to rotate downwards with our heroine clinging to it. How fast is the heroine traveling in m/s when she hits the canyon wall?
Details and assumptions
- The acceleration of gravity is − 9 . 8 m/s 2 .
- Treat the heroine as a point mass.
- Neglect air resistance.
The answer is 19.8.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
6 solutions
I am too dumb.. I solved it by calculating various inertias and rotational energy and so on. :D
Nice solution!
Log in to reply
I feel like this question baits people into using rotational motion, but I always look to see if I can solve problems using forces and energy first since they are the simplest.
can someone please post a solution not by energy method but by rotational motion ??
I had the same idea, but I made up my solution with 30 meters instead of 20!
i used v^2=u^2+2as where u=0, a=9.8, s=20
Very impressive!!
This is very nice, but I'm a little confused. We just covered rolling motion in school and I thought that kinetic energy had to be split into translational and rotational? Why can we simply use a single 'V' in this problems?
So weird... so much useless info...
Wait. Why doesn't the answer come when we use Rotational Mechanics? The bridge, modelled as a rod, pivoted at leftmost point, suffers a decrease of PE as its center of mass descends by 15m. So it gains both rotational and translational Kinetic energy. The girl suffers decrease of PE as it descends by 30 m and gains kinetic energy. But the answer does not come.
Log in to reply
There is a rotational mechanics solution that someone else posted below this. In the end, rotational mechanics and energy should yield the same answer.
Moment of inertia of the bridge-heroine system about the point from where the bridge is hanging = (m1l^2)/3 + m2r^2 I = (500 30 30)/3 + 70 20 20 I = 178000 kgm^2 Work done by gravitational Torque dW = Ƭ sinө dө Total work done W = ʃ(0toπ/2) Ƭ sinө dө = ʃ(0toπ/2)(m1gr1 + m2gr2)sinө dө W = [(20 70 9.8)+(15 500 9.8)] (0-(-1)) = 87220 By work energy theorem W = ΔK.E. ½ Iω^2 = 87220 So; ω = 0.99 rad/s Velocity of heroine = r2 ω So; v = 20*0.99 v = 19.8 m/s
In this system, the total energy is conserved. As a result, M b r i d g e g h c m , b r i d g e + M p e r s o n g h p e r s o n = 2 1 ( I b r i d g e + M p e r s o n ( 3 2 L ) 2 ) ω 2 .
ω is the final angular velocity of the bridge and the person when they reach the canyon wall.
h c m , b r i d g e is the center of mass height above the final center of mass position of the bridge.
h c m , p e r s o n is the height of the person above the final position of the person.
I b r i d g e is the moment of inertia of the bridge about an axis at its end.
Using this equation, you can solve for ω to be approximately 0 . 9 9 0 r a d / s e c . .
The tangential velocity of the person would then be ω ( 3 2 L ) = 1 9 . 8 0 9 m / s .
I too tried that way I of bridge should be 1/3ML^2 and not 1/12 ML^2 isn't it?
Log in to reply
Yes, the moment of Inertia for a rod rotating at its center of mass is 1/12ML^2 and since the bridge is rotating with respect to and end, yes, it should be I = 1/3 ML^2
What is the numerical value for h_cm,bridge??
Let's isolate the bridge from the hero. First, calculate the bridge's final velocity: P E i + K E i = P E f + K E f m g h = 2 m v 2 2 g h = v 2 The bridge has uniform velocity, so we can treat it as a point of mass located in the center of the bridge. v 2 = 2 g h = 2 × g × 1 5 m = g × 3 0 m The same way, we find the hero's velocity squared to be g × 4 0 m . They both have the same angular velocity, so that means one does not depend on the other. The hero's velocity is then: 9 . 8 m / s 2 × 4 0 m ≈ 1 9 . 7 9 m / s
Because potential and kinetic energy are conserved, P E i = K E f . Or, in other words, m g h = 2 m v 2 and v = g h . In this case, since he is 3 2 of the way, the radius - or height - is 3 2 ( 3 0 m ) = 2 0 m . Thus, v = 9 . 8 1 ( 2 0 ) = 1 9 . 8 0 9 .
Both the solutions here miss crucial aspects of the problem. The key notion here is that the heroine and the bridge make up one rigid body that is rotating. Hence one needs to consider conservation of energy, but with total angular kinetic energy rather than translational. Hence we want to avoid statements about "uniform velocity" etc. and talk about "uniform angular velocity". Anyone have a correct, condensed solution?
This is a relatively simple problem requiring just excessive calculations. Let mass of Bridge be M and heroine be m. Let she cling at a spot r from the center of rotation of the bridge. As length of bridge is l=30 m. I am taking reference level for calculation of P.E from that point Initial Mechanical Energy= Mg 30 +mg 30. Final M. E= Mg 15 + mg (30-2/3*30) +1/2 I Omega^2....the last tem is due to M.I. Equate both sides and the asnwer is obtained...
Sun traverse 180 degree in 12 hours and sun and moon are separated by half a degree so it will take approx 2 minutes
Solution using energy:
The total distance that the heroine falls once the bridge hits the wall is 20 meters since the heroine is standing 2/3 the way across a 30 meter bridge.
We know that after the fall, all of the potential energy after 20 meters will be converted to kinetic energy.
m v 2 / 2 = m g h via conservation of energy.
v 2 = 2 g h * after cancelling the mass. Note: mass is irrelevant in this problem.
* v = 2 × 9 . 8 m e t e r s / s e c o n d 2 × 2 0 m e t e r s after taking the square root of both sides
The final answer for velocity comes out to 19.8 meters/second .